


7 Exemples d'utilisation
Nous présentons dans ce chapitre deux exemples d'utilisation de SPPoC dans des contextes différents : la génération de code et l'estimation de
volumes de communication.
Ces exemples illustrent différents aspects de SPPoC : le premier fait
exclusivement appel à de la programmation linéaire et à des
traitements sur les résultats fournis par PIP ; le deuxième est
beaucoup plus complet et illustre la nécessité et l'efficacité des
simplifications intermédiaires.
7.1 Génération de code
L'exemple que nous présentons ici illustre la partie de SPPoC qui
permet la programmation linéaire en nombres entiers, à savoir
l'interface à PIP et le calcul sur les QUAST. Le problème consiste à
générer un code d'itération qui parcourt les points d'une union de
domaines paramétrés. Ces domaines ainsi que l'ensemble de définition
des paramètres sont définis par des ensembles de contraintes affines.
Comme expliqué dans [1], résoudre ce genre de problème
permet de générer du code après transformation d'un nid de boucles à
contrôle statique par n'importe quelle suite de transformations
affines (ordonnancements linéaires, affines, affines par morceaux,
placements par projection, tuilage, torsion, etc). La méthode utilisée
permet de traiter les nids de boucles non parfaitement imbriqués avec
des transformations différentes pour chaque instruction.
7.1.1 Modélisation
L'idée de base consiste à ne pas essayer de reconstruire un nid de
boucle, mais de construire un code à base de conditionnelles et de
sauts, comme on peut les trouver dans le code assembleur provenant de
la compilation de boucles. Il suffit en fait de calculer deux
fonctions : l'une, first, qui donne le premier point de
l'itération, c'est-à-dire le minimum lexicographique du domaine
considéré ; et l'autre, next, qui calcule le point suivant le
point courant. Ce point suivant est le minimum lexicographique de tous
les points du domaine d'itération qui sont plus grands
lexicographiquement que le point courant. Si le domaine d'itération
est
L(z)= {x Î Zn | $ y Î Zm, Ax+By+Cz£ d}
(4)
où m, n, p, q ÎN*, AÎ Zp×Zn, BÎ Zp×
Zm, CÎ Zp× Zq et dÎZp, avec z un vecteur de
paramètres à valeurs dans un polyèdre D={zÎ Zq | Ez£
f},alors le calcul de next revient à résoudre le problème :
trouver le x' minimum vérifiant les contraintes :
|
|
ì
ï
í
ï
î |
|
| z Î D |
| x Î L(z) |
| x' Î L(z) |
| x < x' |
|
ì
ï
í
ï
î |
|
| Ez£ f |
| Ax+By+Cz£ d |
| Ax'+By'+Cz£ d |
| x < x' |
|
(5) |
La difficulté de cette résolution tient au fait que la contrainte
x< x' n'est pas linéaire. Pour la linéariser, on utilise la
définition de l'ordre lexicographique pour décomposer cette contrainte
en une disjonction :
|
|
| |
x1 < x'1 |
| ou |
x1 = x'1, x2 < x'2 |
| |
·
·
· |
| ou |
x1 = x'1, ..., xm-1 = x'm-1, xm < x'm
. |
|
(6) |
La recomposition des résultats des différents sous-problèmes linéaires
est simplement le calcul du minimum de ces sous-problèmes. Or, comme
ces différents résultats peuvent être ordonnés (conséquence directe de
la décomposition de l'ordre lexicographique), nous pouvons utiliser
ici la fonction EQuast.group qui optimise le calcul du minimum
dans ce cas précis (voir section 6.4).
7.1.2 Exemple de résolution
Nous considérons un nid de boucles sur les indices 0£ i£ n et
0£ j£ i qui est transformé en un nid de boucles sur les
indices i et k=i+j.
Nous avons deux problèmes linéaires à résoudre correspondants à la
disjonction de l'ordre lexicographique. Définissons d'abord la partie
commune des systèmes de contraintes :
# let pc = <:s<0<=n; 0<=i<=n; 0<=j<=i; k=i+j;
0<=i'<=n; 0<=j'<=i'; k'=i'+j'>>;;
val pc : SPPoC.System.t =
{n >= 0, i >= 0, i <= n, j >= 0, i >= j, i+j = k, i' >= 0, i' <= n,
j' >= 0, i' >= j', i'+j' = k'}
On veut obtenir i' et k' en fonction de i et k. Pour cela, il
nous faut résoudre en considérant que i', k', j' et j sont des
variables et i, k et n des paramètres. Nous devons ensuite
supprimer les dimensions j et j' inutiles. Ceci peut être fait en
utilisant la question Question.min_lex_exist <:v<i',k'>>
<:v<j',j>>. La construction des deux problèmes linéaires à
résoudre se fait alors comme suit :
# let p1 = PIP.make (System.combine pc <:s<i<i'>>)
(Question.min_lex_exist <:v<i',k'>> <:v<j',j>>);;
val p1 : SPPoC.PIP.t =
Solve : MIN(i', k', j', j)
Under the constraints :
{n >= 0, i >= 0, i <= n, j >= 0, i >= j, i+j = k, i' >= 0, i' <= n,
j' >= 0, i' >= j', i'+j' = k', i > i'}
# let p2 = PIP.make (System.combine pc <:s<i=i';k<k'>>)
(Question.min_lex_exist <:v<i',k'>> <:v<j',j>>);;
val p2 : SPPoC.PIP.t =
Solve : MIN(i', k', j', j)
Under the constraints :
{n >= 0, i >= 0, i <= n, j >= 0, i >= j, i+j = k, i' >= 0, i' <= n,
j' >= 0, i' >= j', i'+j' = k', i = i', k > k'}
Nous calculons ci-dessous les deux résultats intermédiaires et nous
les combinons pour obtenir le QUAST étendu représentant la
fonction next :
# let r1 = PIP.solve p1;;
val r1 : SPPoC.EQuast.t = if i-n <= -1 then [1+i; 1+i] else _|_
# let r2 = PIP.solve p2;;
val r2 : SPPoC.EQuast.t = if 2*i-k >= 1 then [i; 1+k] else _|_
# let next = EQuast.group System.empty r1 r2;;
val next : SPPoC.EQuast.t =
if i-n <= -1 then [1+i; 1+i] else if 2*i-k >= 1 then [i; 1+k] else _|_
La fonction first se calcule aisément comme suit :
# let first =
PIP.solve (PIP.make <:s<0<=n; 0<=i<=n; 0<=j<=i; k=i+j>>
(Question.min_lex_exist <:v<i,k>> <:v<j>>));;
val first : SPPoC.EQuast.t = [0; 0]
Nous pouvons maintenant en déduire un pseudo-code d'itération :
i=0;
k=0;
BOUCLE:
-- corps de la boucle --
if n-i >= 1 then
i=i+1;
k=i+1
else
if k <= 2*i-1
then k=k+1
else goto FIN
endif
endif;
goto BOUCLE
FIN:
7.1.3 Compléments
Bien que nous ayons présenté cette génération de code en utilisant
SPPoC de manière interactive, elle est intégrée à un prototype de
paralléliseur automatique développé au PRiSM à l'université
de Versailles. Ce schéma de résolution y a été étendu et optimisé.
Les exemples complets présentés dans [1] ont produit
plusieurs dizaines d'appels à PIP à la minute et ont ainsi permis de
vérifier la robustesse de l'implémentation.
7.2 Estimation de volumes de communications
Un autre exemple d'application utilisant SPPoC est le calcul
d'une estimation du volume de communications générées par
une instruction d'affectation dans un programme HPF.
La méthode est présentée dans [2], nous ne rappelons
ici que les éléments nécessaires pour d'apprécier l'utilité de SPPoC pour ce genre de calcul.
7.2.1 Un exemple pour fixer les idées
Commençons par donner un exemple de programme HPF :
Program MatInit
!HPF$ PROCESSORS P(8,8)
!HPF$ TEMPLATE T(n,m)
!HPF$ DISTRIBUTE T(CYCLIC,CYCLIC) ONTO P
real A(n,m), B(n)
!HPF$ ALIGN A(i,j) WITH T(i,*)
!HPF$ ALIGN B(i) WITH T(i,1)
do i=1,n
do j=1,m
A(i,j)=B(i) (S1)
end do
end do
end
Ce programme se contente d'initialiser une matrice en recopiant un
vecteur dans chacune de ses colonnes. Nous allons chercher à estimer
le volume des communications générées par l'instruction S1. À
ce propos on constate que S1 est une affectation ne concernant
qu'un seul tableau en lecture. Nous nous limiterons ici à de telles
affectations. Il est facile de généraliser par simple addition de
volumes au prix d'une sur-estimation en cas de références multiples
en lecture au même tableau. La figure 1 représente
le flot des données de l'exemple et la figure 2
indique comment le vecteur et le tableau sont alignés sur le
template6 T.
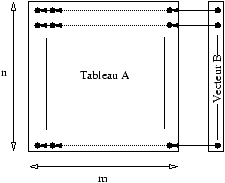
Figure 1: Flot des données
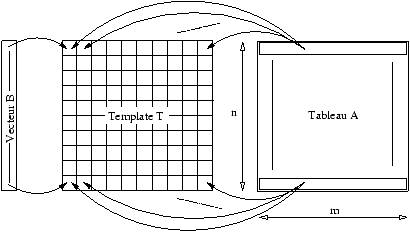
Figure 2: Distribution des objets
La figure 2 montre que les alignements HPF peuvent
être utilisés pour répliquer les données sur le template et donc sur
les processeurs au moyen de « * » dans les directives. Chaque
colonne du tableau A est ici repliquée sur chaque colonne du template
T. Une évaluation du volume de communication doit donc prendre en
compte cette particularité. C'est pourquoi nous comptons les
communications au niveau du template : il y a communication entre deux
éléments de template s'il ne sont pas distribués sur le même
processeur (au sens de la directive PROCESSORS) et si le calcul
d'une valeur alignée sur le premier élément nécessite une valeur
alignée sur le second. Nous définissons le volume de communications
générées par une instruction d'affectation comme le nombre de
communications entre éléments de template générées par cette
instruction.
Des techniques de compilation telles que la vectorisation ou la
factorisation des communications permettent d'éviter certaines des
communications que nous prenons en compte. Cependant notre but est de
donner une estimation pour un programme donné indépendamment du
compilateur ou de la machine utilisée. Grâce à cette estimation il est
possible de choisir une implantation d'algorithme plutôt qu'une autre.
7.2.2 Représentation des alignements et des distributions HPF
Pour donner une formule précise du volume de communications il faut pouvoir
modéliser formellement les alignements et les distributions HPF. Un alignement
HPF peut se concevoir comme la composition de l'inverse d'une fonction
affine avec d'une fonction affine. La fonction inverse permet de formaliser
l'éventuelle réplication de données.
Ainsi l'alignement du tableau A de notre exemple se modélise
par la composition de l'inverse de la fonction
dA ( i1 , i2 )
= i1
et de la fonction
gA ( i1 , i2 )
= i1
.
L'alignement du tableau B est lui modélisé par
la composition de l'inverse de la fonction
dB ( i1 , i2 )
= ( i1 , i2 )
et de la fonction
gB ( i1 )
= ( i1 , 1 )
.
La modélisation d'une distribution HPF se base sur une projection rT
qui permet de sélectionner les dimensions du template qui sont distribuées
sur les processeurs et sur un vecteur de paramètres kT. Les
dimensions du template sont distribuées suivant le schéma
CYCLIC(k)7,
le paramètre k étant donné, pour chaque dimension, par le
vecteur de paramètres. Il est possible d'obtenir une distribution par
blocs en choisissant correctement le paramètre k.
Si les bornes inférieures et supérieures du template et du tableau
de processeurs sont notées Tmin, Tmax, Pmin et Pmax,
la fonction donnant les coordonnées du processeur sur lequel est distribué
un élément de template donné est
pT(J)
=
Pmin+(rT(J-Tmin)÷kT)%(Pmax-Pmin+1)
.
(7)
Dans le cas de notre exemple, la fonction de projection est
rT ( j1 , j2 ) =
( j1 , j2 )
et le vecteur de paramètres
kT = ( 1 , 1 )
.
La fonction de distribution est donc
7.2.3 Formule d'estimation du volume de communications
Pour préciser la formule de calcul du volume de communications telle
que définie dans le paragraphe 7.2.1, nous introduisons
quelques notations :
-
le domaine d'itération englobant l'instruction d'affectation est
appelé D et le domaine de définition du template T est
appelé DT ;
- les fonctions d'accès aux éléments de template FE
(pour le tableau en écriture) et FL (pour le tableau en
lecture) sont définies comme la composition des fonctions
d'alignement et des fonctions d'accès de ces tableaux ;
- la fonction pT est, bien entendu, la fonction de distribution
du template T.
Le volume de communications est alors donné par le nombre d'éléments
de l'ensemble :
|
|
{ |
(I,J) | JÎ DT, IÎFE-1(J),
" KÎ FL(I), pT(J)¹pT(K)
|
} |
(9) |
7.2.4 Utilisation de SPPoC pour le calcul de volume
Notre but est de calculer de façon automatique le cardinal de
l'ensemble décrit par la formule 9. Le présent
paragraphe montre comment SPPoC peut être utilisé pour effectuer les
différentes étapes de ce calcul.
Des opérateurs infixes sont offerts pour manipuler des vecteurs de
formes linéaires. Ce sont les opérateurs arithmétiques et de comparaison
classiques préfixés par le symbole |. Avec ces opérateurs, la
construction des domaines de définition est très facile comme le montre
cet extrait de code :
...
let dt = Polyhedron.of_system
( System.make ( ( j |>= t_min ) @ ( j |<= t_max ) )
...
Les contraintes d'appartenance comme IÎFE-1(J) ne sont pas
exprimables directement par SPPoC . Par contre, il est possible de
construire l'ensemble des (I,J) respectant une telle contrainte.
Pour cela, il suffit de prendre un ensemble paramétrique de paramètre J
défini par la contrainte I=J et de calculer une succession d'images et de
pré-images de cet ensemble par les fonctions composant FE
(les deux fonctions composant l'alignement du tableau en écriture et
la fonction d'accès au tableau en écriture).
Voici un extrait de code de notre prototype de calcul de communications
qui implante ce procédé :
...
Polyhedron.inter
domaine_iteration
( Polyhedron.preimage
( Polyhedron.preimage
( Polydedron.image ensemble_parametrique delta_E )
gamma_E )
phi_E )
...
La contrainte KÎFL(I) se traite de manière analogue.
La fonction de distribution est, elle aussi, implantée sous la forme
d'un système d'équations.
Le plus complexe est le calcul du résultat de la projection rho
et du vecteur de paramètres kappa, SPPoC fait le reste :
...
let taille = p_max |- p_min |+ one in
System.make ( p |= ( p_min |+ (( rho |/ kappa ) |% taille )))
...
Ce système est dupliqué pour pouvoir être appliqué sur J et
sur K, l'égalité entre les deux fonctions de distribution est
assurée par l'utilisation de variables intermédiaires représentant
les coordonnées des processeurs (vecteur p).
Il faut aussi régler le problème de l'opérateur " qui
apparait dans (9). En fait il est préférable,
plutôt que de calculer le nombre d'éléments de template donnant
lieu à une communication, de calculer le nombre d'éléments de
template ne donnant lieu aucune communication.
Calculer le nombre d'éléments de l'ensemble (9)
revient donc à calculer le nombre d'éléments de
|
|
{ |
(I,J) | IÎ D, JÎ DT |
} |
(10) |
|
|
{ |
(I,J) | JÎ DT, IÎFE-1(J),
$ KÎFL(I), pT(J)=pT(K)
|
} |
(11) |
En définitive, l'ensemble (11) s'obtient par calcul
de l'intersection des ensembles présentés plus haut. Le système
résultat comporte des divisions entières et des modulos que SPPoC ne
linéarise qu'en dernier recours. De cette façon, aucune information
n'est perdue ce qui permet des simplifications plus efficaces que dans
un système linéarisé.
Dans le cas de notre exemple MatInit, la session SPPoC ci-dessous
montre à la fois le système correspondant à l'ensemble
(11) et la façon dont il est simplifié.
Pour s'y reconnaître il faut savoir que lors de la génération
automatique du système les notations suivantes ont été utilisées :
-
les composantes de I sont i1 et i2 ;
- les composantes de J sont j1 et j2 ;
- les composantes de K sont k1 et k2 ;
- les composantes du vecteur des processeurs sont p1 et p2 ;
- et enfin les paramètres du programme HPF sont n et m.
# System.simplify
<:v<i1,i2,j1,j2>> (* Variables *)
<:v<n,m>> (* Paramètres *)
<:s< (-1+p1)+(-((-1+j1) mod 8)) = 0,
(-1+p2)+(-((-1+j2) mod 8)) = 0,
(-1+p1)+(-((-1+k1) mod 8)) = 0,
(-1+p2)+(-((-1+k2) mod 8)) = 0,
i1 = j1, k1 = j1, k2 = 1,
m >= j2, j2 >= 1, i2 >= 1,
n >= j1, m >= i2, j1 >= 1 >> ;;
- : SPPoC.System.t =
{i1 = j1, (-1+j2) mod 8 = 0, m >= j2, j2 >= 1, i2 >= 1,
n >= j1, m >= i2, j1 >= 1}
Dans le cas général, il n'est pas possible de compter directement
le nombre de points entiers dans le système simplifié par SPPoC .
En effet, celui-ci peut encore comporter des variables intermédiaires
utilisées pour modéliser le problème (les composantes de K et
de p). Il ne faut compter que les couples (I,J) pour lesquels
il existe un K et un p vérifiant les contraintes de
(11). Cela peut être réalisé par un
appel à PIP pour résoudre le programme linéaire de minimisation
(ou de maximisation cela n'a pas d'importance) du vecteur (K,p)
sous les contraintes de (11). Il s'agit d'une
résolution paramétrique en fonction des paramètres I, J et
des paramètres N du programme HPF. Dans le résultat de PIP seuls
importent les domaines des paramètres I, J et N pour lesquels
existent des solutions au programme linéaire. Le résultat recherché
est la somme des nombres de points entiers dans ces domaines. Il est
évident qu'il faut obtenir le nombre de points entiers en fonction
des paramètres N.
Ce nombre de points est calculé via la fonction
Polyhedron.enumeration de SPPoC . Pour notre exemple, il est
inutile d'appeler PIP puisque la simplification opérée par SPPoC a déjà éliminé les variables intermédiaires. Le résultat
du calcul de la différence entre le nombre de points entiers dans
les ensembles (10) et (11)
est le suivant :
[{({m >= 1, n >= 1},
{ray(n), ray(m), vertex(m+n)})},
7/8*n*m**2-m*n*[0, 7/8, 3/4, 5/8, 1/2, 3/8, 1/4, 1/8]m]
Ce résultat indique qu'il n'existe de communication que si
n³ 1 et m³ 1 (dans le cas contraire l'instruction ne
génère aucune opération, il n'y a donc effectivement pas
de communication). Il est possible de simplifier le résultat
en supposant que m est divisible par 8, dans ce cas le
coefficient périodique vaut zéro. Le nombre de
communications est alors 7/8nm2, résultat auquel
on pouvait s'attendre au vu de la figure 2.








