


| Chapter 6 |
A propos des récurrences |
|
Les récurrences sont très utilisées dans les programmes
numériques. Presque tous les programmes comportent des
sommations d'éléments d'un tableau, des calculs de produits
scalaires, des calculs d'extrema, etc.
Des récurrences plus complexes sont parfois utilisées comme
la recherche d'un élément particulier dans un tableau ou
le calcul des moyennes des éléments en ligne et en colonne
d'une matrice. Or ces récurrences sont, le plus souvent,
mal parallélisées par les compilateurs basés sur la méthode
géométrique. Ce chapitre explique pourquoi et quels remèdes
peuvent être appliqués.
| 6.1 |
Les récurrences et la parallélisation automatique |
|
Il y a du parallélisme implicite dans un programme dès que
l'ordre d'exécution de certaines de ses opérations peut être
changé sans modifier son résultat final. Ce genre de commutativité
peut avoir deux sources différentes.
-
La première source est relative à l'utilisation des cellules
mémoires ; les permutations possibles sont définies par les
conditions de Bernstein. Les paralléliseurs actuels (tels que
PAF) exploitent uniquement ce type de commutativité.
- La seconde source de commutativité est relative aux propriétés
algébriques des opérateurs apparaissant dans le programme. Pour
extraire le parallélisme lié à ces propriétés une
``parallélisation sémantique'' (terme dû à P. Jouvelot)
est nécessaire.
Par exemple le calcul de la somme
est usuellement implanté par les quelques lignes ci-dessous.
INTEGER i,n
REAL s,x(1000)
s=0.
DO i=1,n
s=s+x(i)
END DO
Un paralléliseur ordinaire
1
déclare que cette boucle est séquentielle à cause de la dépendance
PC sur s. En conséquence, même sur une machine parallèle cette
boucle s'exécutera en un temps de l'ordre de n. Cependant comme
l'addition est associative et commutative
2,
le calcul de la somme peut être fractionné en plusieurs sous-sommes
portant sur n/p éléments (où p est le nombre de
processeurs). Il suffit ensuite de cumuler les sommes partielles.
Le temps d'exécution du calcul est donc de l'ordre de
n/p+log2p.
Il est donc important pour un compilateur d'exploiter le parallélisme
implicite des calculs tels que (6.1). Deux étapes sont
nécessaires. La première étape consiste à repérer toutes les
récurrences. Comme la plupart des langages ne disposent pas de notations
pour désigner des calculs comme (6.1), les récurrences sont
exprimées à l'aide de boucles. Il faut donc reconnaître les boucles
utilisées pour calculer des récurrences. Cela devient compliqué
pour des programmes comportant des boucles emboîtées et manipulant
des tableaux (surtout des tableaux multi-dimensionnels). La seconde
étape consiste à vérifier que la récurrence est efficacement
implantable sur une machine parallèle. Ceci revient à vérifier
que la fonction associée à la récurrence respecte certaines
propriétés. Actuellement, l'unique moyen de réaliser ce test
est d'utiliser une reconnaissance de forme. L'efficacité de la
reconnaissance de forme, en terme de rapidité d'exécution,
est liée à la taille de la base de règles. D'où l'intérêt
de réduire cette taille au minimum en normalisant les récurrences,
c'est-à-dire en normalisant le programme source. En fait notre
but est de chercher à détecter uniquement des récurrences
simples (i.e. des récurrences définies par une seule instruction
d'affectation). Il faut donc savoir dans quelle mesure les récurrences
d'un programme complexe peuvent être ramenées à des récurrences
simples par normalisation du programme.
Pour mener à bien ce travail, il faut connaître précisément les
récurrences qui peuvent s'exécuter sur une machine parallèle.
Il est aussi nécessaire de définir la notion de récurrence
dans un programme écrit dans un langage impératif. Nous verrons
que cela conduit à la fois à étendre la notion de récurrence
(e.g. comme nous manipulons des tableaux de valeurs, nous introduirons
le concept de récurrence multi-directionnelle) et à la réduire
(e.g. nous imposons des contraintes drastiques sur la fonction
associée à la récurrence).
| 6.2 |
Parallélisation de récurrences |
|
Pour l'instant nous ne cherchons pas à préciser la notion de
récurrence dans un programme impératif, mais juste à
caractériser les différents calculs, regroupés sous le
nom de calculs de récurrence, qui peuvent être exécutés
plus vite sur une machine parallèle que sur une machine
séquentielle.
Les récurrences qui peuvent être calculées efficacement sur
des machines parallèles sont celles qui peuvent être implantées
à l'aide d'un opérateur Ä binaire et associatif.
La récurrence s'écrit :
|
é
ë |
|
|
s(0) |
= |
a(0) |
|
" iÎ Nn*, |
s(i) |
= |
s(i-1)Ä a(i) |
|
|
s=a(0)
DO i=1,n
s=s Ä a(i)
END DO
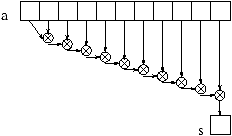
Les opérations sont alors effectuées comme indiquées sur le
schéma ci-dessous.
Dans ce cas de figure une seule opération peut être exécutée
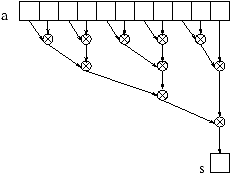
à la fois. En fait, il est possible, grâce à l'associativité
de Ä de réordonner les opérations suivant un arbre binaire
de calcul comme montré sur le schéma suivant :
Cette fois plusieurs opérations peuvent être exécutées en
parallèle. Sur une machine avec un nombre illimité de processeurs,
il est possible d'effectuer le calcul en log2(n) étapes.
Pour une machine réelle, les n données sont réparties sur
les p processeurs et seule l'étape finale de traitement des
résultats partiels s'effectue suivant un arbre binaire de calcul.
Le temps d'exécution est alors de n/p+log2(p).
Si p est petit et que la machine parallèle utilisée n'est pas
adaptée au parallélisme à grain fin, il est avantageux d'implanter
en séquentiel l'étape finale. En effet, le surcoût de la
distribution du travail aux p processeurs masque alors le gain dû
à la parallélisation. Le temps d'exécution est alors de l'ordre
de n/p+p.
Dans le cas où toutes les valeurs de la récurrence sont utiles
la récurrence est appelée un scan
4.
Un programme séquentiel pour calculer le scan est :
s(0)=a(0)
DO i=1,n
s(i)=s(i-1) Ä a(i)
END DO
Il est possible de calculer un scan en parallèle. Une première
passe utilise le même arbre binaire de calcul que celui de
la réduction. La seconde passe effectue une remontée dans
l'arbre pour mettre à jour les résultats partiels (pour plus
de détails voir par exemple [12]). Sur une machine
avec p processeurs la complexité du calcul du scan est
toujours de l'ordre de n/p+log2(p). Par contre comme
deux parcours de l'arbre binaire sont nécessaires, le temps
de calcul d'un scan est deux fois plus grand que celui d'une
réduction.
Dans la suite de cette thèse les mots réduction et scan
désigneront toujours des récurrences associées à des
opérateurs associatifs, c'est-à-dire des récurrences
calculables efficacement sur une machine parallèle.
La parallélisation de réductions et de scans ne fait pas
l'unanimité dans le monde du calcul numérique. Le fait est
que les additions et les multiplications informatiques ne sont
pas vraiment associatives. La parallélisation des réductions
et des scans peut donc conduire à des résultats numériques
légèrement différents. Dans le cas de méthodes de calcul
itératives, la différence de résultat peut conduire à un
ralentissement de la convergence (voire à un programme ne
convergeant plus). En fait, c'est plutôt le contraire qui risque
de se passer. Il a été montré, à l'aide d'un modèle probabiliste
[46] que le calcul d'une somme suivant un arbre binaire est,
la plupart du temps, plus précis que le calcul séquentiel.
Il n'est donc pas du tout évident que la parallélisation des
réductions et des scans nuise à la convergence d'un calcul.
Dans le cas où l'opération est l'addition, le calcul est même
plus précis.
Certains travaux présentent des méthodes pour paralléliser
des récurrences utilisant des fonctions non-associatives
(e.g. [17]). Ces travaux se basent sur le fait que
la composition des fonctions ° est, elle, associative.
L'inconvénient est que ° est une opération très
difficile à implanter et qui peut conduire à des tailles de
fonctions croissant de façon exponentielle. La parallélisation
est alors fictive car les opérations de base du programme parallèle
ont une complexité beaucoup plus grande que celles du programme
séquentiel.
| 6.3 |
Les définitions du terme récurrence |
|
Tout d'abord un point de vocabulaire. Dans cette thèse il est constamment
question de récurrences ; il faudrait parler, en toute rigueur, de ``suites
récurrentes''. Cependant nous utiliserons le terme ``récurrences'' car
il est désormais très largement répandu.
Notre but est de détecter des récurrences dans des programmes
numériques. Un point délicat est de savoir quelles récurrences
il est nécessaire de traiter, ce qui revient à donner une définition
de la notion de récurrence dans les programmes impératifs.
Il est logique de chercher une définition mathématique des récurrences.
Il est assez frappant de constater qu'il n'en existe pas qui réponde
à nos besoins. Les récurrences sont utilisées dans de nombreuses
disciplines mathématiques mais ne sont presque jamais formalisées.
Quand elles le sont c'est dans le cadre d'une étude bien précise.
Citons, par exemple, la définition d'une récurrence trouvée dans
un cours de mathématiques ([35]). Dans cet ouvrage une
récurrence est une suite (un)n³ 0 vérifiant :
" nÎ N, un+k=ak-1 un+k-1+ ··· + a0 un
,
où les ai sont des complexes et a0 est non nul.
Cette définition est trop restrictive. Seules les récurrences
à base d'additions sont envisagées or nous avons vu que toutes
les récurrences que l'on peut calculer à l'aide d'une opération
binaire et associative peuvent être efficacement parallélisées.
De plus l'espace de calcul de la récurrence est une suite au sens
strict. C'est à dire, d'un point de vue informatique, un tableau
uni-dimensionnel. Une récurrence, dans un programme, peut avoir un
espace de calcul plus complexe à cause des tableaux multi-dimensionnels.
En fait la définition la plus adaptée à notre problème est celle
du lambda-calcul ([6]). Une récurrence y est décrite comme
la donnée de deux lambda-expressions M et N et d'une fonction
p. La première valeur de la récurrence, notée R 0 est
la valeur de l'expression N. La valeur de rang n est donnée
par la formule
R n=M n ( R p(n)) .
Notez que la fonction M, dite fonction de propagation, est aussi
paramétrée par l'indice n.
Cette définition peut être étendue aux récurrences d'ordre
supérieur à 1. Une récurrence est alors la donnée d'un tuple
(M,N1,...,Nk) et d'une fonction p. Les k premières valeurs
de la récurrence sont les expressions N1 à Nk. Un terme de
rang n supérieur ou égal à k est donné par la formule
R n=M n ( R p(n)) ( R p2(n)) ... ( R pk(n))
,
où l'élévation à la puissance s'entend en terme de composition
de fonctions. Cette définition est la formalisation de la définition du
dictionnaire Larousse qui indique qu'une récurrence est une suite
``dont le terme général s'exprime à partir de termes le précédant''.
C'est la fonction p qui joue le rôle de fonction prédécesseur.
D'un point de vue informatique cette fonction prédécesseur
associe à chaque terme de la récurrence la variable dans laquelle
il doit être stocké.
Il est évidemment impossible de détecter toutes les récurrences
qui suivent cette définition. Pour s'en convaincre il suffit
de considérer un programme quelconque P s'exécutant sur une
machine donnée M. Ce programme peut être calculé par
la récurrence telle que :
-
le terme N1 est le couple constitué de l'état mémoire
de M avant l'exécution de P et de la première itération de
P ;
- la fonction M associe à un couple constitué d'un état
mémoire m et d'une opération o un couple constitué de l'état
mémoire m après l'exécution de o et de l'opération suivant o
dans l'ordre du programme P.
C'est d'ailleurs cette récurrence qui est à la base de la sémantique
dénotationelle [33] et de la sémantique opérationnelle.
Il est donc sans objet de chercher à détecter
toutes les récurrences.
Seules doivent l'être les récurrences qui peuvent être efficacement
parallélisées, c'est-à-dire celles présentées dans la section
6.2 et définies par le système (6.2).
Ceci impose donc qu'une fonction binaire et associative puisse être
extraite de la fonction de propagation de la récurrence.
De plus seules les fonctions d'ordre 1 seront considérées. Il est
par contre possible de transformer certaines récurrences d'ordre
supérieur en récurrences d'ordre 1.
Considérons par exemple la récurrence d'ordre 2 ci-dessous.
|
é
ê
ê
ë |
|
|
s(0) |
= |
0 |
| |
s(1) |
= |
1 |
|
" iÎ {2,...,n}, |
s(i) |
= |
a(i).s(i-1)+b(i).s(i-2)+c(i) |
|
|
é
ê
ê
ë |
| |
S(1) |
= |
|
|
" iÎ {2,...,n}, |
S(i) |
= |
|
|
Enfin, une autre caractéristique de la récurrence (6.2) est
que sa fonction prédécesseur (i.e. i|® i-1 sur N) est
bijective. Les récurrences possédant des fonctions prédécesseur
non bijectives sont donc écartées.
Considérons la récurrence ci-dessous :
DO i=1,n
DO j=1,n
s(i,j)=s(i,j-1)+s(i-1,j)+s(i,j)
END DO
END DO
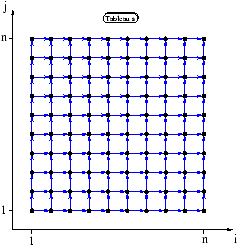
Le graphe des dépendances du programme est illustré par le
schéma suivant :
La fonction prédécesseur de cette récurrence est :
p(i,j)={ (i,j-1), (i-1,j) }
.
Il ne s'agit pas d'une fonction bijective, cette récurrence ne peut
s'exprimer à l'aide d'un système tel que (6.2).
Même avec ces restrictions le problème est encore trop compliqué.
En effet, sans autre hypothèse, toute sous-récurrence de la
récurrence définissant le programme entier et possédant une
fonction prédécesseur bijective convient.
Dans le cas général, la fonction prédécesseur opère
donc sur les opérations du programme. Dans la section 5.3
il a été vu que ces opérations sont de la forme (i,v), avec
i le label d'une instruction et v un vecteur d'itération.
Les récurrences portant sur plusieurs instructions (donc potentiellement
sur différents tableaux) seraient donc admises.
Il est possible de tirer directement une récurrence du programme suivant :
t(0)=0
DO i=1,n
s(i)=t(i-1)+a(2*i-1) (v1)
t(i)=s(i)+a(2*i) (v2)
END DO
Les labels v1 et v2 sont les labels de la seconde
et de la troisième instructions d'affectation du programme.
Les termes de la récurrence sont indicés par les opérations
(v1,i)iÎNn* et
(v2,i)iÎNn*.
La fonction prédécesseur est définie par cas :
|
|
| " iÎ{2,...,n}, p((v1,i))=(v2,i-1)
et, |
| " iÎ{1,...,n}, p((v2,i))=(v1,i)
. |
|
|
|
| " iÎ{2,...,n}, M((v1,i),x)=x+a(2i-1)
et, |
| " iÎ{1,...,n}, M((v2,i),x)=x+a(2i)
. |
|
Des récurrences calculées suivant des trajectoires
les plus bizarres seraient aussi admises.
Le programme suivant représente une récurrence :
s(0)=0
DO i=1,n
s(i*i)=s((i-1)*(i-1))+a(i) (v1)
END DO
La fonction prédécesseur est :
|
" iÎ{2,...,n}, p((v1,i))=
(v1 |
,(i |
|
-1)2)
.
|
" iÎ{2,...,n}, M((v1,i),x)=x+a(i)
.
Le problème est que la fonction de propagation n'est pas
manipulable avec les outils de l'algèbre linéaire.
Il n'est pas réaliste d'essayer de détecter des récurrences
avec de telles fonctions de propagation. Dans le cas de récurrences
sur plusieurs instructions cela nécessiterait d'appliquer une
reconnaissance de forme sur tous les sous-ensembles des corps
de boucles. La combinatoire est trop élevée surtout sachant que
chaque opération élémentaire (une reconnaissance de forme) a
un coût exponentiel.
Comme, de plus, les programmes que nous étudions ont des fonctions
d'indices affines, la fonction prédécesseur est limitée
à des expressions affines.
Par contre nous n'imposons pas que la fonction de propagation définisse
un ordre < total sur les termes de la récurrence. Ceci élargit la
définition classique de récurrence. En fait, cela permet de décrire
un ensemble de récurrences. Soit º<|
la relation d'équivalence qui indique si deux termes de la récurrence sont
comparables par <. Une récurrence classique est associée à
chaque classe d'équivalence du quotient de l'ensemble des termes
par º<|.
Deux récurrences sont définies par le programme ci-dessous.
DO i=2,n
a(i)=a(i-2)+a(i) (v1)
END DO
En effet deux classes d'équivalence sont définies
(v1,i)i pair et
(v1,i)i impair.
Dans le même ordre d'idée, n récurrences sont définies
par le programme :
DO i=1,n
DO j=1,n
a(i,j)=a(i-1,j)+a(i,j) (v1)
END DO
END DO
Les classes d'équivalence sont paramétrées par j :
ce sont les (v1,(i,j))iÎNn*.
En résumé, il est raisonnable de détecter, par reconnaissance de
forme, des récurrences :
-
dont les termes ne sont constitués que d'opérations d'une
instruction ;
- dont la fonction de propagation est définie par des expressions
affines (ou affines par morceaux) en les compte-tours des boucles
englobantes et des paramètres de structure du programme.
Comme de plus, dans le cadre de cette étude, seuls les scans ou les
réductions nous intéressent il faut se limiter aux récurrences
telles qu'une fonction binaire et associative peut être extraite de
la fonction de propagation.
Par contre aucune restriction n'est faite sur le domaine de définition
des indices des termes de la récurrence. Il peut s'agir d'un espace
à plusieurs dimensions (contrairement à la définition classique
des récurrences). En outre, la définition de récurrence est
élargie pour permettre la description de récurrences
paramétrées.
| 6.4 |
État de l'art de la détection de récurrences |
|
Des travaux ont déjà été menés sur la détection de récurrences,
ou plus exactement sur la détection de réductions. L'article
[37] présente une méthode basée sur une exécution
symbolique (``symbolic stores'') du corps des boucles du programme.
Dans [47] une méthode s'appuyant sur le graphe des dépendances
est envisagée. Enfin l'article de Callahan [14] décrit
une transformation de programmes adaptée à la parallélisation de
récurrences quelconques.
| 6.4.1 |
Méthode basée sur l'exécution symbolique |
|
L'évaluation symbolique est un procédé qui permet de résumer
l'effet d'un ensemble d'instructions d'affectation. Cela revient à
remplacer plusieurs instructions d'affectation par une seule instruction
d'affectation multiple.
L'évaluation symbolique des trois affectations
x=z+2
t=2*x+z
z=sqrt(t)+x
donne pour la variable x la valeur z+2, pour la variable
t la valeur 2*(z+2)+z et pour la variable z la valeur
sqrt(2*(z+2)+z)+z+2. Il faut noter que les valeurs contiennent encore
des variables d'où le terme d'évaluation symbolique ; les expressions
sont manipulées comme des chaînes de caractères.
L'évaluation symbolique peut être étendue pour traiter les
instructions conditionnelles (par exemple en transformant ces
instructions en expressions conditionnelles).
La première étape de la méthode de détection de réductions
par évaluation symbolique est justement l'évaluation symbolique
des corps des boucles les plus internes. Une reconnaissance
de forme est alors appliquée sur les valeurs symboliques obtenues
pour reconnaître les réductions. Les nids de boucles peuvent être
traités par propagation des réductions détectées.
Le principal avantage de cette méthode est que le programme est
normalisé durant l'évaluation symbolique. Ainsi le résultat
de la détection est relativement indépendant des différentes
manières dont un algorithme peut être implanté (une simplification
des valeurs symboliques doit tout de même être effectuée).
L'évaluation symbolique du corps de la boucle
s=0
DO i=1,n
t=s+a(i)
s=t+b(i)
END DO
donne pour la variable s la valeur s+a(i)+b(i).
Une reconnaissance de forme peut alors s'apercevoir que s
contient, en fin de boucle, la somme des a(i)+b(i).
Par contre un inconvénient de l'exécution symbolique d'un programme
est que les tableaux ne sont pas correctement pris en compte. Par exemple
a(i) et a(j+1) sont des chaînes de caractères
différentes mais peuvent représenter la même cellule mémoire
si i est égal à j+1.
De ce fait certaines réductions échappent au détecteur.
Dans l'exemple suivant
DO i=2,n
a(i)=b(i-1)+a(i)
b(i)=a(i-1)+b(i)
END DO
une analyse symbolique n'est pas capable de constater que
si i³ 3 alors la valeur affectée à a(i) est :
a(i-2)+b(i-1)+a(i)
En conséquence la réduction ci-dessous n'est pas détectée :
DO i=3,n
a(i)=a(i-2)+b(i-1)+a(i)
END DO
Comme expliqué dans la section 6.3, cette récurrence
contient en fait deux récurrences, une pour les i pairs et
une pour les i impairs.
De la même façon les réductions implantées avec plusieurs
boucles échappent à la détection.
Une analyse symbolique du programme ci-dessous échoue à
détecter la réduction qu'il contient.
DO i=1,n
DO j=1,m
s(j)=t(j)+a(i,j)
END DO
DO k=1,m
t(k)=s(k)
END DO
END DO
En effet s(k) et s(j) sont des symboles différents ;
l'analyse symbolique ne peut pas se rendre compte que l'effet d'une
itération de la boucle externe consiste à ajouter à chaque
t(k) la valeur de a(i,k).
De plus l'imprécision due à l'analyse symbolique peut conduire
à remplacer, à tort, une portion de programme par le calcul
d'une réduction. Pour éviter ces erreurs un test
est utilisé pour sélectionner les corps de boucles dans
lesquelles la détection peut s'effectuer sans risque.
Comme le problème est complexe, le test est souvent pessimiste,
c'est-à-dire qu'il vérifie une condition suffisante mais pas
nécessaire. En conséquence encore plus de réductions passeront
entre les mailles de la détection.
Il est illégal de dire que les tableaux x
et y du programme
DO i=2,n
x(i)=x(i-1)+y(i-1)
y(i)=y(i-1)+2*x(i-1)
END DO
peuvent être calculés par les deux réductions
ci-dessous :
DO i=2,n
x(i)=x(i-1)+y(i-1)
END DO
DO i=2,n
y(i)=y(i-1)+2*x(i-1)
END DO
Un moyen de s'en rendre compte est d'analyser les dépendances
du programme initial.
| 6.4.2 |
Méthode basée sur le graphe de dépendance |
|
Pour pouvoir détecter des récurrences au vu du graphe de
dépendance (GD), il faut trouver un moyen de représenter
les boucles du programme dans ce graphe.
Un tel moyen est décrit dans [47].
En premier lieu, les boucles sont déroulées jusqu'à obtenir
une forme normale. Une boucle est en forme normale quand chacune
de ses itérations utilise des éléments de tableaux et des
variables scalaires assignés dans l'itération elle-même
ou dans la précédente.
Par exemple, la forme normale de la boucle
DO i=1,n
x(i)=x(i-2)+x(i)
END DO
est
DO i=1,n,2
x(i)=x(i-2)+x(i)
x(i+1)=x(i-1)+x(i+1)
END DO
Quand la forme normale est atteinte, un GD générique de la
boucle est construit (i.e. un GD résumant la boucle). Puisque
la boucle est en forme normale, l'union du GD de l'itération
initiale avec celui d'une itération intermédiaire et avec
celui de l'itération finale donne une image exacte de la
boucle entière. Ensuite, une reconnaissance de forme est
appliquée au GD de la boucle, et pour chaque sous graphe
qui décrit une récurrence, une portion de code appropriée
est générée. Une telle méthode permet une meilleure
détection (e.g. détecte des récurrences croisées).
Son principal inconvénient est l'absence d'une normalisation
systématique. La normalisation du programme est sensée se
faire par les transformations classiques (substitution de temporaires,
expansion de scalaires, inversion de boucles, etc.).
Le choix des transformations à effectuer et de l'ordre d'application
est un problème ouvert ; actuellement seules des heuristiques sont
connues.
De plus comme la reconnaissance de forme s'applique au GD dans son
ensemble la complexité temporelle de la détection augmente
rapidement avec la taille du programme en entrée.
Une dernière limitation est que la forme normale pour les boucles
n'existe que dans le cas de dépendances uniformes.
Ainsi la boucle ci-dessous ne possède pas de forme normale.
DO i=1,n
x(i)=x(i-k)+x(i)
END DO
En fait cette boucle doit être considérée comme étant le
calcul de k récurrences.
| 6.4.3 |
Méthode basée sur une transformation de code |
|
Cette méthode n'est pas limitée aux réductions mais
s'applique aux récurrences en général. Il existe une
limitation, cependant ; les fonctions de propagation des
récurrences doivent être des fonctions affines.
La première étape consiste à extraire les récurrences
brutes du programme initial. L'auteur suppose que ces récurrences
sont de la forme :
DO i=1,n
Ai1=fi1(Ai-11)
...
Air=fir(Ai-1r)
END DO .
Une normalisation préliminaire du programme est donc sous-entendue.
De plus cette forme ne prend en compte que des tableaux uni-dimensionnels,
il n'est pas sûr que cette méthode puisse s'étendre facilement à des
tableaux multi-dimensionnels.
Dans une seconde étape une reconnaissance de forme très simple
est utilisée pour vérifier que les fonctions (fik)kÎNr*
sont bien affines en les variables (Aik)kÎNr*.
La dernière étape est une transformation de code astucieuse
de la boucle initiale. Sans entrer dans les détails, il suffit de remarquer
que le vecteur (Ai1,...,Air) est donné par une récurrence
matricielle d'ordre 1 (le procédé est identique à celui utilisé
pour paralléliser la récurrence (6.3) dans la section
6.3).
Comme le produit de matrices est associatif, du parallélisme peut être
extrait. De plus pour réduire le coût de la méthode, il faut tenir
compte du fait que la matrice utilisée est creuse, donc que certains
calculs peuvent être évités. Le code final peut être exécuté
en un temps O(n/p+p) avec p processeurs.
Par exemple, le programme
DO i=1,n
a(i)=a(i-1)+2*b(i-1)
b(i)=a(i-1)+x(i)
END DO
définit un système de récurrences affines. Donc il peut
être automatiquement transformé en un programme
parallèle équivalent (C est le nombre d'itérations à calculer
sur un processeur, c'est-à-dire é n/p ù) :
DO ALL i=0,n,C
A(0,i)=[0,1,0]
B(0,i)=[0,0,1]
DO k=1,C
A(k,i)=A(k-1,i)+2*B(k-1,i)
B(k,i)=A(k-1,i)+[x(i+k),0,0]
END DO
END DO
DO i=C,n,C
a(i)=A(C,i-C)*[1,a(i-C),b(i-C)]
b(i)=B(C,i-C)*[1,a(i-C),b(i-C)]
END DO
DO ALL i=1,n,C
DO k=1,C
a(i+k)=A(k,i)*[1,a(i),b(i)]
b(i+k)=B(k,i)*[1,a(i),b(i)]
END DO
END DO
Notez que les opérations de base du programme parallèle
sont maintenant des opérations sur les vecteurs. Les crochets
([ et ]) sont utilisés comme constructeurs de vecteurs.
Cette méthode présente l'avantage d'avoir une phase de
reconnaissance de forme réduite à sa plus simple expression.
En fait cette méthode est plus une transformation source à source
qu'une véritable détection de récurrences. Ce manque d'analyse
conduit à la génération d'un code avec un surcoût important.
Dans l'exemple précédant le programme parallèle exécute 23
opérations arithmétiques (additions et multiplications) dans une
itération et le programme séquentiel seulement 3 pour le même
travail. Aussi pour obtenir une accélération de 2 il faut, au
minimum, 16 processeurs.
L'extraction de récurrences simples de systèmes récurrents
complexes peut réduire ce surcoût. De plus la méthode ne donne
aucune indication sur la manière d'extraire les récurrences brutes.
En conclusion la méthode de Callahan pour paralléliser les
récurrences affines et la méthode de détection de récurrences
présentée dans cette thèse sont complémentaires. La méthode
de Callahan peut être utilisée après notre phase de normalisation
du programme initial. La phase de normalisation améliore l'efficacité
du code généré puisqu'il éclate les systèmes récurrents
complexes en systèmes plus simples.
- 1
- Quelques compilateurs commerciaux peuvent reconnaître des
formes classiques et donc compiler efficacement ce genre d'exemple.
- 2
- En négligeant les erreurs d'arrondi.
- 3
- Le terme vient du langage de programmation APL.
- 4
- Il s'agit encore d'un terme lié au langage APL.







 p(i,j)={ (i,j-1), (i-1,j) } .Il ne s'agit pas d'une fonction bijective, cette récurrence ne peut s'exprimer à l'aide d'un système tel que (6.2).
p(i,j)={ (i,j-1), (i-1,j) } .Il ne s'agit pas d'une fonction bijective, cette récurrence ne peut s'exprimer à l'aide d'un système tel que (6.2).

