Previous Contents Next
Chapter 5 PAF, un exemple de compilateur parallèle
L'équipe de parallélisation automatique du laboratoire PRiSM (Parallélisme, Réseaux, Systèmes et Modélisation) de l'université de Versailles et Saint-Quentin possède son propre compilateur parallèle. En s'appuyant sur la description de ce compilateur (nommé PAF, acronyme pour Parallélisation Automatique de Fortran) nous présentons ici un panorama des techniques de parallélisation automatique. PAF est composé de plusieurs modules écrits soit en C soit en LeLisp (une variante de Lisp). Les interactions entre les différents modules sont décrites par la figure ci-dessous.

5.1 Le langage d'entrée
Le compilateur PAF prend, en entrée, des programmes écrits en un sous-ensemble de Fortran 77. Ce sous-ensemble est connu sous le nom de langage à contrôle de flot statique. La seule structure de contrôle d'un tel langage est la boucle DO. Les instructions peuvent être des affectations simples ou conditionnelles, voire des instructions d'entrée-sortie. Les appels à des procédures peuvent être autorisés, mais les paramètres sont considérés comme modifiés par l'appel. De plus les bornes des boucles DO ne doivent dépendre que des comptes-tours des boucles englobantes et des paramètres de structure. Ces paramètres sont des entiers initialisés par une instruction de lecture et non modifiés dans le reste du programme. Enfin, pour pouvoir utiliser tous les outils de l'algèbre linéaire, les fonctions d'indices apparaissant dans les tableaux doivent être affines. Il est possible de prendre en compte les structures de contrôle de type if-then-else si leurs prédicats respectent les mêmes règles que les bornes de boucles. Sinon il est toujours possible de les transformer en instructions d'affectation gardées (voir [56]). Une propriété importante des programmes à contrôle statique est que leur nombre d'opérations est connu dès que les paramètres de structure sont connus. En ce qui concerne PAF, les programmes Fortran sont immédiatement traduits dans une représentation intermédiaire (RI). La RI représente un programme avec des structures de type liste plus faciles à manipuler par les modules écrits en Lisp. Le module de traduction F2L est écrit en C.
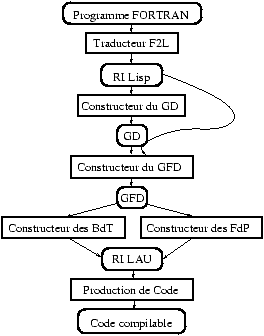
Considérons l'exemple suivant que nous allons retrouver tout au long de cette section. 
PROGRAM relax
INTEGER n,m,i,j
REAL a(100,100)
DO i=1,n
  DO j=1,m
    a(i,j)=f(a(i-1,j),a(i,j-1))   (v1)
  END DO
END DO
END
La représentation intermédiaire qui lui correspond est 
(df relax nil
    (prog ()
      (integer n nil) (integer m nil)
      (integer i nil) (integer j nil)
      (real a (100 100))
      (real f nil)
      (for (i 1 1 n)
        (prog ()
          (for (j 1 1 m)
            (prog ()
              (aset a i j
                (f (aref a (- i 1) j)
                   (aref a i (differ j 1))))))))))
5.2 Analyse des dépendances
Le second module de PAF à entrer en action est le module d'analyse de dépendances. Nous avons vu dans 4.2 que les dépendances peuvent être représentées par un graphe (GD). Dans ce graphe un arc entre deux opérations indique que les deux opérations sont en conflit. Le graphe est orienté. Par convention l'opération source est plus petite que l'opération destination au sens de <. Il est impossible de construire le graphe de dépendance pour toutes les opérations d'un programme (ce graphe est appelé le graphe détaillé des dépendances). En effet une simple boucle peut représenter n opérations où n est un paramètre de structure du programme. La solution est de calculer un graphe générique, chaque sommet représentant un ensemble d'opérations. Un sommet du graphe calculé par le constructeur du GD de PAF représente une instruction du programme source. Le calcul des dépendances revient à résoudre des systèmes de contraintes affines en nombres entiers. Pour résoudre ces systèmes, le compilateur PAF utilise le logiciel de programmation linéraire paramétrique et en nombres entiers PIP [25]. Pour réduire le temps de calcul, d'autres compilateurs utilisent des méthodes approchées comme les tests de Banerjee, la méthode d'élimination de Fourier-Motzkin ou l'algorithme du simplexe (ces deux dernières trouvent des solutions rationnelles).
Le GD générique du programme relax ne comporte qu'un sommet v1. La liste de ses arcs est : 
(v1 v1 PC (aref a i j) (aref a (- i 1) j))
(v1 v1 PC (aref a i j) (aref a i (- j 1)))
Chaque arc comporte la source et la destination de la dépendance, le type de la dépendance et les références aux cellules mémoires sur lesquelles porte la dépendance. Le schéma correspondant est :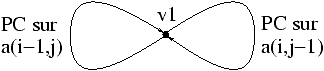
Le graphe des dépendances met en lumière les conflits entre opérations, mais ce n'est pas forcément la structure de choix pour la détection du parallélisme. En effet ce graphe présente deux défauts :
5.3 Analyse du flot des données
Pour pallier au manque de précision du GD classique, PAF calcule le graphe du flot des données. Les sommets de ce graphe représentent toujours des instructions mais les arcs ne sont définis que pour un sous-ensemble des opérations d'une instruction. Une opération peut être définie formellement comme un couple (i,v) constitué d'un label et d'un vecteur d'itération. Il existe un label par instruction et chaque composante du vecteur représente le compte-tour d'une boucle englobante. Le graphe du flot des données (GFD) n'indique pas comme le GD les ensembles d'opérations en conflit mais met en évidence le flux des données entre les différentes opérations. C'est la seule information réellement utile pour la parallélisation automatique ; l'ordre partiel <// ne doit mettre en relation deux opérations que si l'une produit des données utiles à l'autre. Le module de construction du GFD de PAF donne pour un ensemble d'opérations (i,v)vÎ D 1 les opérations calculant les valeurs lues par cet ensemble. Les sources des valeurs sont données sous la forme d'un quast, c'est-à-dire un arbre de sélection dont chaque feuille est une forme quasi-affine. Une forme quasi-affine est une forme définie à partir des opérations d'addition, de multiplication par une constante et de division entière par une constante.
Le GFD du programme relax est : 
Source de a(i-1,j) dans v1 ;
   * IF [ (i-2>=0) ] -> (v1,i-1,j)
Source de a(i,j-1) dans v1 ;
   * IF [ (j-2>=0) ] -> (v1,i,j-1)
Ce graphe est composé d'un sommet v1 portant deux boucles :
Le GFD permet de transformer un programme à contrôle statique en un programme à assignation unique (plus de détails seront donnés en 7.1.1). Dans un tel programme il n'y a plus de réutilisation des variables, il ne reste que des dépendances du type PC. Un ordre partiel <// moins contraignant peut donc être trouvé. Le programme est mieux parallélisé, par contre la taille de la mémoire utilisée est bien plus importante.

5.4 Ordonnancement et placement
Le GFD donne un bon ordre partiel respectant la sémantique du programme source. Encore faut-il pouvoir exploiter cet ordre, c'est à dire générer un code parallèle. Pour cela deux informations relatives aux opérations sont nécessaires. Quand peut-on les exécuter et où ? Le calcul d'une base de temps (BdT) répond à la première question puisqu'elle donne la date d'exécution de chaque opération. Il ne s'agit que d'une date logique car il n'est pas possible de calculer exactement à quel top d'horloge l'opération doit se déclencher (plus de détails sur le calcul de la base de temps seront vus en 11.1). Le second problème est résolu par le calcul d'une fonction de placement (FdP). De manière analogue un placement donne le numéro du processeur logique sur lequel une opération doit s'exécuter. La fonction de placement tente de minimiser le coût des communications. Le coût est estimé en fonction du volume de données à transférer. Dans le compilateur PAF une heuristique est employée ; seule la dimension du volume de données est prise en compte. Enfin, un repliement des processeurs logiques sur les processeurs physiques à la HPF doit être employé pour obtenir un placement pour une machine réelle. D'un point de vue technique, le compilateur PAF calcule les bases de temps et les fonctions de placement sous la forme de quasts. Ces fonctions ne retournent pas forcément un scalaire ; il est possible d'avoir des bases de temps et des placements multi-dimensionnels.
La base de temps trouvée par PAF pour le programme relax est :
q(v1,i,j)=i+j-2  .
Cela signifie que toutes les opérations de l'instruction v1 qui se trouvent sur la même anti-diagonale de l'espace d'itération s'exécutent au même instant (voir la figure ci-dessous).
La fonction de placement du programme est :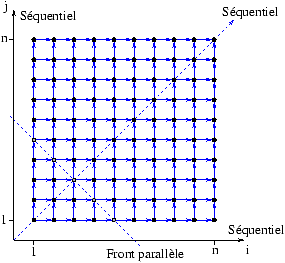
p(v1,i,j)=i-1  .
Toutes les opérations sur une même ligne de l'espace d'itération doivent être placées sur le même processeur pour minimiser le coût des transferts de données. Il est à noter que la fonction de placement p(v1,i,j)=j-1 convient aussi, puisque le GFD est symétrique par rapport à la diagonale de l'espace d'itération. Ces deux placements minimisent les communications car l'une des deux données nécessaires à un calcul est située sur le processeur exécutant ce calcul. Évidement, une solution encore meilleure du point de vue de la minimisation des communications, est d'exécuter toutes les opérations sur le même processeur, mais plus aucun parallélisme n'est alors possible. Une des difficultés du calcul des fonctions de placement est justement d'éviter cette perte de parallélisme.
Le compilateur PAF synthétise les résultats du GFD, du module de calcul de la base de temps et du module de calcul de la fonction de placement dans un seul fichier au format LAU (i.e. langage à assignation unique).

5.5 Génération de code
La dernière étape de la compilation d'un programme par PAF est la génération d'un programme parallèle. La méthode utilisée est la méthode géométrique (dite méthode de la transformation espace-temps). Comme expliqué dans la section 4.3, cette transformation est en fait un changement de base du domaine d'itération des nids de boucles. La base de départ est définie à partir des comptes-tours du nid initial. La nouvelle base est celle définie par les composantes de la base de temps (donnant lieu à des boucles séquentielles) et les composantes de la fonction de placement (donnant lieu à des boucles parallèles). Les caractéristiques de la matrice de passage sont importantes. Si la matrice est uni-modulaire (matrice à coefficients entiers de déterminant 1 ou -1), l'espace transformé peut encore être vu comme l'ensemble des points entiers d'un polyèdre. Il existe alors des méthodes pour trouver un nid de boucle énumérant ces points [5]. Dans le cas contraire tous les points entiers du polyèdre ne sont pas itérés. Il est possible de parcourir tous les points et de garder les instructions d'affectations mais cela produit un surcoût qui peut aller jusqu'à masquer le gain obtenu par la parallélisation. La bonne méthode est de trouver les pas des boucles du nouveau nid qui permet de n'itérer que les points utiles [20]. Un second problème est que la méthode de base ne trouve le nouveau nid de boucle que pour une instruction. Pour trouver un nid itérant les opérations de toutes les instructions, une solution est de calculer l'enveloppe convexe des espaces d'itérations. Cette fois encore le surcoût dû aux itérations de points inutiles peut conduire à une décélération par rapport au programme séquentiel.
Il suffit de remarquer que l'union convexe de deux segments perpendiculaires est un plan ; le nombre de points à itérer peut passer de n à n2.
La solution est de ne pas construire l'enveloppe convexe et de générer des nids de boucles différents pour chaque espace d'itération [16, 18]. Pour l'instant le compilateur PAF peut générer du code pour la CM-2 [51], pour le Cray Y-MP [40] et pour la MasPar [18].
La relation entre la base de temps, la fonction de placement et les compte-tours des boucles du programme relax est :
æ
è
q(v1,i,j)
p(v1,i,j)
ö
ø		 = é
ë
1 1
1 0
ù
û		 æ
è
i
j
ö
ø		 + æ
è
-2
-1
ö
ø		  .
La matrice de passage est uni-modulaire donc le programme parallèle peut être généré avec des boucles de pas 1 : 
DO t=0,2*n-2
  DO ALL p=max(0,t-n+1),min(n-1,t)
    a(p+1,t-p+1)=f(a(p,t-p+1),a(p+1,t-p))
  END DO
END DO
Le programme ci-dessus pour être complet devrait expliciter les communications entre les processeurs. Il peut cependant s'exécuter sur une machine avec une mémoire partagée. Le nouvel espace d'itération est décrit par la figure suivante.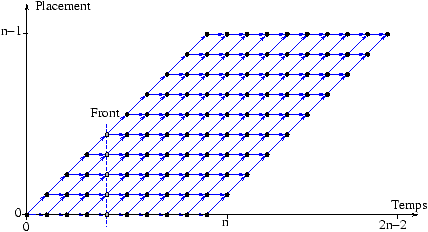
5.6 Recherches récentes
Nous venons de survoler les principales phases du compilateur PAF. Des recherches récentes ou en cours ont pour objet d'étendre le domaine d'application de ce compilateur. La première extension concerne le langage des programmes source. Les travaux de Pierre David [21] montrent qu'un sous-ensemble de C comprenant les pointeurs peut être utilisé. La contrainte imposant que les fonctions d'indices soient linéaires a été levée en partie par Alain Dumay [22]. Certains programmes à contrôle dynamique (utilisation de boucles while) sont maintenant traités [18]. Le module de calcul du flot des données a été optimisé et trouve désormais des sources sous une forme plus générale que les simples quasts [7]. Enfin, comme le compilateur PAF lui-même n'effectue aucune analyse inter-procédurale, Jean-Yves Berthou a mis au point un prototype de compilateur pour des programmes scientifiques de grande taille [11]. Ce prototype analyse (sur des jeux d'essais) le programme complet et en extrait les noyaux, c'est à dire de courtes portions de code contenant un haut degré de parallélisme implicite. Ces noyaux sont ensuite parallélisés par le compilateur PAF.

1
PAF impose que l'ensemble D soit un polyèdre convexe.
Previous Contents Next