Overview of the Method

2 Overview of the Method

2.1 What is a Reduction?

A reduction -- the name comes from the APL language [6] -- is any operation which takes a set of values as argument and gives a single value in return². Most often, a reduction is defined as the repeated application of a binary function to the elements of the input set in some order:

s = f(... f(a₁,a₂),..., a_n). (1)

Specially interesting is the case where f is an associative function. Commutativity and the existence of a unit are also useful. With the help of these properties, definition (1) can be rearranged in various ways in order to exhibit parallelism. As a rough estimate, reduction of n values on P processors takes about n/P + log₂ P units of time.

APL was the first language to introduce a specific notation for reduction. In contrast, ordinary imperative languages, new and old, have no such feature. In Fortran, for instance, one has to write:

Program reduc
s = a(1)
do i = 2,n
  s = f(s,a(i))
end do
end

and the situation is similar for C or Pascal. With the advent of massively parallel computers, there is a strong incentive to extract the last ounce of parallelism from sequential programs, hence the importance of detecting associative reductions.

The reader must be warned that some computer operators are only approximately associative. For instance, addition of floating point numbers is associative up to rounding errors. In such cases the algorithm must be subjected to a stability analysis before applying reduction parallelization.

2.2 Detecting a reduction

The question is now to identify code such as in program reduc where a reduction is concealed in a sequential program.

It is not too difficult to identify code such as:

    do i = ...
      s = f(s)
    end do

The question is then whether the assignment may be rewritten as

      s = g(s, e(i))

with g an associative operation. This is a difficult mathematical question. Usually, the associativity of a binary operation has to be proved, and such a proof may be of arbitrary difficulty. Since it is not possible, at least with present technology, to include a theorem prover in a compiler, the obvious solution is to use instead a catalog of predefined reductions and to match this knowledge base against the object program. This is done in many commercial parallelizers, which are able to recognize elementary reductions like sums and dot products.

Such recognition of reductions by pattern matching is more complicated than it looks: consider for example the problem of summing the components of a vector. It may be written in many different ways, among which:

program A              program B                 program C
s = 0.                 s = a(1)             1    s = 0.
do i = 1,n             do i = 2,n                do i = 1,n
    s = s + a(i)           s = a(i) + s     2       t = s + a(i)
end do                 end do               3       s = t
end                    end                       end do
                                                 end

Furthermore, most of the time, the summation loop above will be polluted by extraneous code, which may interfere -- or not -- with the summation. It would need a very large knowledge base to recognize all these forms as equivalent.

As is well known, the solution is normalization of the object program. Ideally, all equivalent programs should transform into the same normal form and the reduction detection should be done on the normal form. This is clearly impossible, since it would give an algorithm for testing the equivalence of two programs, which is undecidable as soon as the programming language is powerful enough. The way out is both to restrict the input language -- to static control programs in our case -- and to accept imperfect normal forms, in which some but not all equivalent programs have the same normalization.

For instance, with the system which is described in this paper, program A and C will normalize to the same form, but program B will not. This is as it should be, since program A and B are equivalent only if n ³ 1. But even adding this information will not enable us to have program A and B converge to the same normal form, unless we use the powerful transformations which are described in Sect. 5.

Many researchers have defined normal forms for use in reduction detection and other program transformations. The best known one is obtained by symbolic execution [7]. When the presence of a reduction in a loop is suspected, its body is submitted to an interpreter which do all calculations algebraically. Consider for instance program C, and let s_i, t_i be the values of s and t at the beginning of iteration i of the loop. Similarly, let s_ki, t_ki be the values of these variables after execution of statement k in iteration i. Symbolic interpretation of statement 2 and 3 gives successively:

t_2i	=	s_i + a(i)
s_3i	=	s_i + a(i)

At this point, one starts the next iteration, meaning that s_i+1 = s_3i. We have thus found the recurrence:

s_i+1 = s_i + a(i) .

Programs A and B would lead to the same recurrence. Note that adding extraneous statements to the loop (e.g. resetting a(i) to zero after statement 3) would not change the above result, thus showing that this modification does not affect the reduction.

This method is quite powerful and can be extended to handle conditional statements in the loop body [8]. It needs a formal algebra system and its power is directly proportional to the normalization power of this system. However, it cannot handle either reductions on arrays or arrays of reduction (i.e. systems of recurrence equations).

Callahan [1] has proposed a method which can handle systems of reductions provided they are linear (i.e. their solution reduces to matrix products). The basic idea is similar to symbolic execution, but the interpreter handles only linear right hand sides. Variables which are the result of non linear calculations are treated as undefined, and the undefined value has to be propagated across the symbolic calculation. At the end of the process, the linearly computed variables at the end of one iteration are expressed as functions of their values at the beginning of this iteration. Computing their final value is equivalent to compute a succession of matrix products, which is associative. Most of the time, the iteration matrix is sparse: Callahan gives methods to exploit this fact in order to minimize the total computation time.

The method of [12] is quite different. The aim here is to normalize the dependence graph of the loop. Since the size of the dependence graph of a loop which is iterated n times is at least O(n), this is impossible in general. The authors propose a limited unfolding of the loop body until periodic patterns become apparent. The recognition of reductions is done on this unfolded graph.

Our aim here is to improve on the symbolic execution method in order to be able to handle reductions on arrays as well. Ideally, the following program

    program D
    real a(0:100)
    s(0) = 0.0
    do i = 1,n
        s(i) = s(i-1) + a(i)
    end do

should have the same normal form as program A.

2.3 Normalization Strategy

Our basic requirement is that the representation of a program must be a well defined mathematical object, which can be transformed by applying usual algebraic rules, the most important one being substitution of equals for equals. This requirement is satisfied in a limited way by symbolic execution: in a basic bloc, the value of a scalar variable after the execution of a statement is a mathematical expression, which can be subjected to ordinary algebraic calculations. This is no longer true if one is interested in arrays and if one wants to handle several loops as a whole.

In that case, one has to switch to a representation by a system of recurrence equations in the manner of [13]. An object in such a system is the value of a variable at a well defined point in the execution of a program (a statement and a set of counters for the surrounding loops). The system gives relations between these values. Solving the system is tantamount to running the program.

Fortunately, static control programs with affine subscripts and loop bounds can be automatically converted to system of -- affine -- recurrence equations by dataflow analysis (see section 3.1). The Dataflow Graph, however is not a sufficiently powerful normal form for reduction recognition. For instance, while programs A and D have the same DFG, this is not true for program C. 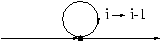In fact the DFG's of all simple reductions we want to recognize -- e.g. the one in program D -- have a very simple form which is depicted in the following figure:

The only cycle in the graph is a loop and the source to sink transformation is a translation. If a DFG has cycles which are not loops, we may try to shrink them by eliminating variables by forward substitution. We will show later that this is not always possible, and give a necessary and sufficient condition for this strategy to succeed.

When a loop is found, one may try to identify a reduction by matching the associated equation with the knowledge base. We will see in Sect. 4 that, while this process basically is pattern recognition, once the pattern has been established, we may use sophisticated techniques for filling in the details.

A program may have a large number of reductions. Once one of them is found, we must set it aside, as it where, and try to find other ones. This may be done simply by introducing a new operator, Scan, which has the same relation to reduction as the integral sign ò has toward integration: it allows one to give a name to an object which is not always expressible in closed form within the underlying theory. The ò and Scan operators share many interesting properties. For instance, a computation on a domain may be split into computations on a partition of this domain.

In graphical terms, introducing a Scan operator allows one to delete the loop on the corresponding node. When this is done, one may continue eliminating variables until other loops are found. This is best done working from inside outward, as in that way the simplest reductions will be detected first.

The result of this analysis is a new version of the Dataflow Graph in which as many reductions as possible have been identified. The result may still be simplified by combining reductions to build higher order reductions. Consider for instance, the program

    program E
    s = 0.0
    do i = 1,n
      do j = 1,i
        s = s + a(i,j)
      end do
    end do

As a first step, we find that the j loop is a sum. The next step is to analyze the i loop, thus finding another summation which uses as data the results of the j loop summations. These results may be combined to give -- we use here the ordinary mathematical notation:

s =

i=1

j=1

a_ij .