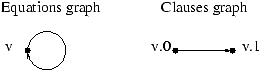Program normalization

3 Program normalization

3.1 Translation to SLRE

A first stage of normalization is achieved by translating the static program (written, for example, in a subset of Fortran) into a system of linear recurrent equations. The equations of the systems we deal with are of the following form:

zÎ D_e, v_e(z)=Exp

_e(v

e₁

(I₁(z)), ...,v

e_n

(I_n(z))) .

The set (v_e)_{eÎ S} represents the variables of the system (let this system be denoted by S). The definition domain of the equation D_e is convex and the (I_k)_kÎ{1,...,n} are affine subscripts functions. Lastly, the expressions Exp_e are conditional functions such that:

Exp_e(z)=

ì
ï
í
ï
î

Exp_e¹(z)	if zÎ D_e¹
· · ·
Exp_e^m(z)	if zÎ D_e^m

The Exp_e^j are classical mathematical expressions (after recurrence detection these expressions may include scan operators). We deal only with sub-domains D_e^j which are convex and are a partition of the definition domain D_e ³. We say that Exp_e(z) is an m clauses expression. In the sequel of this paper, the abstract SLRE representation (3) is mostly used for proofs and algorithms but for examples it is more convenient to use a textual representation.

In the textual representation a system like:

v₁(i,j)= ì
í
î

a(i) if i-j£ 1

1 if i-j = 0

0 if i-j³ 1

is written :
v1[i,j] = case 
            { i-j <= 1 } : a[i] ; 
            { i-j = 0 }  : 1 ;
            { i-j >= 1 } : 0 ;
          esac
This notation is very close to the language Alpha ([11]), a language used to describe systolic systems. This representation is also close to the input language required by our recurrence detector.

3.2 Elimination of Variables Using Substitutions

The last phase of a scan detection method is always a pattern matching. Moreover we want an efficient detection scheme, hence our pattern matching deals only with single variables and not sets of variables. The advantages are plain: smaller set of patterns and lower execution run-time. The main drawback is that recurrences defined by more than one variable cannot be found. Now, recurrences computations often use temporary variables which lead to recurrences defined by several variables, therefore a system normalization must be provided to collapse multi-variables recurrences onto single-variable ones if possible.

Our system normalization can be described as a variant of Gauss elimination. The difference is that the variables we remove are not scalars but arrays whose values are defined by QuASTs.

The recurrence defined by the system below is a two-variables one:
v1[i] = case 
        { i | i = 1 } :       0 ;
        { i | 2 <= i <= n } : v2[i - 1] + a[i] ;
       esac ;
v2[i] = case 
        { i | i = 1 } :       0 ;
        { i | 2 <= i <= n } : v1[i - 1] + b[i] ;
       esac ;
If our pattern matching is directly applied no scan can be detected since there is no self-referencing variable. In fact the recurrence can be detected directly by pattern-matching only if you consider the two variables as a whole. Our solution is to remove either v1 or v2 from the system. For example we replace the reference to v2 in v1 by its definition:
v1[i] = case 
        { i | i = 1 } :       0 ;
        { i | i = 2 } :       0 ;
        { i | 3 <= i <= n } : v1[i - 2] + b[i - 1] + a[i] ;
       esac ;
The variable v1 is now self-referencing (with stride 2) and a mere pattern matching can point out that v1 is to be computed using two addition-scans operating on the data b[i-1]+a[i]. Going from the first to the second system is not a simple textual substitution, We had to compute the expression v2[i-1] from the definition of v2 in the initial system, then substitute it into the definition of v1, then simplify the result. See [16] for details.

We want our scan detector to handle scans on multi-dimensional arrays. In this context another problem arises: scans can be computed along very different paths in these arrays (one may, for instance, compute scan following ellipses). The problem of detecting scans along arbitrary paths is intractable, hence we deal only with rectilinear ones. An uni-directional scan gathers its data following a mere vector. Note that an uni-directional scan associated with a multi-dimensional array represents in fact an array of scans:

The following program computes an array of scans along the diagonals of the array a:
DO i=1,n
 DO j=1,n
  a(i,j)=a(i-1,j-1)+a(i,j)
 END DO
END DO
The uni-directional scan underlying this code has direction vector (

1

1
).

Several detection schemes can be used according to the required precision. The simplest algorithm consists in considering the system of equations as a whole and removing as much variables as possible with our Gauss elimination variant. At this point most of the recurrences are defined by only one variable and a pattern matching can take place. The drawback of this method is that it is not always possible to collapse a recurrence on a single variable using forward substitutions. Hence our elimination process may not be very efficient.

No scan can be extracted from the following system using this simple scheme:
v1[i,j] = case
           { i, j | i=1, j=1 }        :  0 ;
           { i, j | 2<=i<=n, j=1 }    :  v2[i-1,m] ;
           { i, j | 1<=i<=n, 2<=j<=m }:  v1[i,j-1] + a[i,j] ;
          esac ;
v2[i,j] = case
           { i, j | 1<=i<=n, j=1 }    :  v1[i,m] ;
           { i, j | 1<=i<=n, 2<=j<=m }:  v2[i,j-1] + b[i,j] ;
          esac ;
But the third clause of v1 and the second of v2 compute sets of scans. In fact the elimination fails because the recurrences defined by this system are cross-referencing (cannot be computed in parallel).

A more complex detection scheme can be designed using multistage eliminations. The principle is to consider only some references (i.e. equations between our multi-dimensional variables). In a first stage only the references related to the innermost loops of the original program are taken into account. This is equivalent to generate a parametric program for each innermost loop and normalize it (the parameters are those of the original program plus the counters of the surrounding loops). Then pattern matching is applied and closed forms are introduced for the detected scans. In the second stage we add to the graph the references relative to the loops just surrounding the innermost ones. A normalization and a pattern matching are performed again and so on. In this way the elimination is obviously more efficient and we can detect more complex scans (see section 4.1). Indeed, since closed forms appear during the detection process, pattern matching may be applied on variable already defined as a scan. In most cases this denote a scan whose path is piecewise rectilinear, a multi-directional scan.

Our previous example can be handled if the counter i relative to the outermost loop is considered as a parameter. In this context no elimination is to be performed since the only remaining references are the self-referencing ones in the last clauses of v1 and v2. Let sum be the textual equivalent of the å operator, closed forms can be introduced for the scans:
v1[i,j] = case
           { i, j | i=1, j=1 }        :  0 ;
           { i, j | 2<=i<=n, j=1 }    :  v2[i-1,m] ;
           { i, j | 1<=i<=n, 2<=j<=m }:  v1[i,1]+sum(j>=2,a(i,j)) ;
          esac ;
v2[i,j] = case
           { i, j | 1<=i<=n, j=1 }    :  v1[i, m] ;
           { i, j | 1<=i<=n, 2<=j<=m }:  v2[i,1]+sum(j>=2,b(i,j)) ;
          esac ;
It is very important to note that the closed forms are parametric with respect to i.

A difficult technical issue for the multistage elimination scheme is to characterize the references to be taken into account. Indeed, at the system of equations level, there is no longer information about the loop nests. The solution is the notion of reference pseudo-depth. Let the reference to an equation v2 in an equation v1 be of the form:

" zÎ D, v1(z)=...v2(I(z))... .

The pseudo-depth is the greatest integer p such that :

" zÎ D, I(z)[1..p]=z[1..p] .

To normalize only the loops deeper (strictly) than the p level it suffices to consider the references of pseudo-depth greater or equal than p.

Proof:: Only circuits of references can cause the elimination process to fail. The references of pseudo-depth greater or equal to p which are not references relative to the loops at level strictly greater than p cannot be included in a circuit.

The following algorithm summarizes the steps of the multistage elimination method:

Algorithm 1 Scans Detection

Let S be a SLRE.
For pseudo-depth p from the maximum nesting level to 0 :
1. Compute the system graph of S keeping only references of pseudo-depth greater or equal to p.
2. Compute the strong components of this sub-graph.
3. Try a total variable elimination on the components.
4. Apply pattern matching when the total elimination succeeds and rewrite the detected scans with closed forms.
5. Remove inter-components references of pseudo-depth greater or equal to p using substitutions.

3.3 Criterion for Total Elimination

The goal of our elimination phase is to collapse the recurrences defined by several variables into recurrences defined by only one variable. The tool we use to perform the transformation is forward substitution. With this operation we are sure that a system is transformed into an equivalent one. In this section we give a criterion which insures that our elimination process can shrink its recurrences into single variables.

To introduce our proof let us consider a classical system of equations. In such a system the n variables are defined like:

ì
ï
ï
ï
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
ï
ï
ï
î

x₁=f₁(x

k₁¹

,...,x

m₁

)

·
·
·

x_i=f_i(x

k₁ⁱ

,...,x

m_i

)

·
·
·

x_n=f_n(x

k₁ⁿ

,...,x

m_n

)

We do not make any assumption on the functions (f_i)_iÎ_N (in this context forward substitution is really the only operation we can use on the system). Such a system can be represented using a graph. The vertices are the n variables and there is an edge from v_i (corresponding to x_i) to v_j (corresponding to x_j) if x_i appears in the definition of x_j. This graph is similar to the dependence graph of the original program. 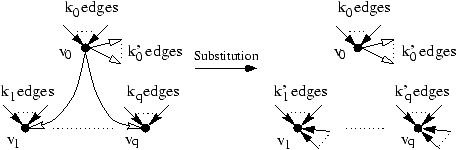The effect of a forward substitution on the graph of the system can be formalized. Let us consider the effect of the substitution of v₀ into v₁, v₂, ..., v_q. The edges from v₀ to the other vertices are removed and new predecessors are added to the targets (those of v₀). Note that the new number of predecessors of, for instance, v₁ is not exactly known, it is only possible to say that this number k'₁ is between max(k₁,k₀) and k₁+k₀. Indeed some of the predecessors of v₀ may also be predecessors of v₁, and are counted once.

Thanks to this technical background we can now figure out the systems that can be normalized. It is easy to verify that if the elimination process succeeds on a system, the only circuits of its graph are then loops (i.e. circuits including a single vertex).

Theorem 2 [Sufficient Condition for a Total Elimination] If the circuits of a strongly connected system ⁴ have a common vertex then the elimination process succeeds on the system.

Proof:: Without the edges going out of the common vertex the system graph is acyclic. Hence a topological sort can be performed on this sub-graph. The result of this sort is a partition of the vertices into sets S₁,...,S_p. At this point one can substitute the definitions of the variables in S₁ into the definitions of the variables in S₂. These variables are now only in terms of the common vertex. Repeating the forward substitutions until S_p lead to fold all the circuits into the common vertex.

Theorem 3 [Necessary Condition for a Total Elimination] The elimination process succeeds on a strongly connected system only if its circuits have a common vertex.

Proof:: The sketch of the proof is as follows. Let G be a strongly connected graph such that for each vertex v of G there is a circuit which does not include v. We show that a graph G' obtained from G by applying some forward substitutions include a strong component with the same properties as G. Moreover such a strong component has at least two vertices, hence it has a circuit of length greater or equal to 2.

Let us now detail the proof. The basic property of transformation by forward substitutions is that if v^- is a predecessor of v in G, either v^- or its predecessors in G are predecessor(s) of v in G'. This implies a conservation property on paths. More precisely if there is a path p in G, then there is a sub-path of p in G which starts with the first or the second vertex of p and stop at the last vertex of p. A special case arises when the path p is in fact a circuit. In this case there is at least one circuit in G' which includes only vertices from p. From the conservation property on paths and circuits, another conservation property can be deduced on inter-circuits paths. Let c₁ and c₂ be two circuits of G, for each circuit c'₂ built from c₂ in G', there is a path from a circuit built from c₁ in G' to c'₂.

Since each circuit of G' built from a circuit of G has as predecessor (via a path) at least one of the circuits of G' built from a given circuit of G (remember that G is strongly connected), there is in G' a strong component including at least one of the circuits of G' build from each circuit of G. For each vertex v of this strong component there exists a circuit of the component which does not include v. Indeed since v is not included in at least one circuit c of G, it is not included in the circuits of G' build from c (one of these is necessary in the strong component).

These results apply only to strongly connected systems but they can be adapted for other systems. It suffices to compute the strong components of the system and verify that each component fulfill the requirements. Our elimination criterion formalizes an intuitive thought: it is not always possible to solve a system of equations using only forward substitutions. The criterion is mostly interesting when nothing is known about the functions (f_i)_iÎ_N of the system (4). In other cases methods using more powerful operations than forward substitution are generally used to solve the system.

In the context of linear equations, systems such as (4) can always be solved using, for instance, the Gauss elimination algorithm. But according to our criterion only systems whose circuits have a common variable can be solved. That is not a contradiction since the Gauss algorithm use substitutions and also linear expressions simplification as basic operations. The linear simplification is a powerful tool since it can remove loops from the system graph. For example in the graph of the system below there is a loop on the vertex v₁ corresponding to the variable x₁.

ì
í
î

x₁=4.x₁+x₂

x₂=2.x₁
.
After simplification of the first equation (x₁=-1/3x₂) there is no longer a loop on v₁.

The criterion is also valid for a system of equations like (2). Its graph is more complex since some edges are defined only in a sub-domain of the variable definition domain. This has an influence on the elimination process. Indeed, after a forward substitution, new edges domains are computed using an intersection. If the intersection is void, the edge does not really exist. So the criterion is always sufficient but is no longer necessary. One may also say that the criterion is sufficient and necessary if no simplification of the clause domains occurs.

3.4 Algorithms for Variables Elimination

All algorithms for variable elimination on strongly connected components have the same pattern: find the common vertex of the system graph circuits and use a topological sort to schedule the forward substitutions (as described in theorem (2)). Hence the difficult point is to find the common vertex.

There is a full range of algorithms to perform this operation. Let us begin with a heuristic method, which is not very efficient but very fast (hence it can be integrated into a commercial compiler). We use the fact that a graph without cycle is also without circuit. Hence to find a vertex included in each circuit of a graph G, it suffices to consider each vertex v of G, to remove its outgoing edges and verify that the remaining graph G_v is acyclic. This verification can be done using the cyclomatic number n(G_v)=m'-n'+p', with m' the number of edges of G_v, n' the number of vertices of G_v (the same as the number n of vertices of G) and p' the number of connected components (i.e. 1 since G_v is a connected graph). The number of edges m' of G_v is the number of edges m of G minus the number m_v of v successors. Hence one has to check for each vertex v if the expression m-m_v-n+1 is null. The test complexity is about O(n) but it is only a heuristic since it does not discriminate between cycles and circuits.

This heuristic can be modified into an exact method. It suffices to replace the computation of the cyclomatic number by a depth-first-search to insure that there is no circuit in the graph. This method complexity is of the order of O(n.m).

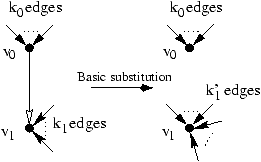
A more efficient method to perform the elimination process is to use basic substitutions. Basic substitutions are forward substitutions for variables used by only one other variable.

In the picture above, the vertex v1 has, after the substitution, a number k'₁ of predecessors such as max(k₀,k₁)£ k'₁£ k₀+k₁. If a basic substitution is applied to a strongly connected graph, there is no circuit including v₀ and the resulting graph restricted to all vertices but v₀ is also strongly connected.

Proof:: The vertex v₀ has no longer successors, so no circuit can include this vertex. Moreover if a path exists between two vertices (different from v₀) before the substitution, it also exists also after (even if the former includes v₀, since it goes through v₁ after the substitution).

When no basic substitution can be applied to a graph, either its strong component is reduced to a vertex and, in the initial graph, every circuit include this vertex, or the strong component include several vertices and a total elimination cannot be performed on the initial graph.

Proof:: If the strong component is a single vertex, the elimination criterion implies that in the initial graph the circuits have a common vertex. Moreover the conservative property on circuits enforces that this vertex is the one in the strong component.

Let G' be a graph obtained from a strongly connected graph G using a basic substitution. Due to the properties of basic substitutions, if the strong component of G' is such that for each of its vertices v there exists a circuit not including v, then G has the same property. Now consider the final component including several vertices. No more basic substitution can be applied, hence each vertex has at least two successors. If a vertex v is removed, the others have still at least one successor, so there exists a circuit which does not include v.

This prove that the sequential application of basic substitutions is as powerful as the application of multiple substitutions in the context of our variable elimination process. An efficient algorithm can be extracted from the method provided that, for each vertex v, a sorted list of its predecessors pred(v) is available.

Algorithm 4 Finding a Common Vertex

For each vertex v, compute its number of successors ns(v) and store one of these in succ(v).
Initialize the stack s with the vertices having a unique successor.
Stop if s is empty or if there is only one vertex in the component.
Unstack v from s. Let v⁺ be the successor in succ(v).
Perform a sorting merge on pred(v) and pred(v⁺), for each v^- belonging to both lists subtract one to its number of successors ns(v^-). When this number is equal to one stack v^- on s.
Store the result of the merging in pred(v⁺) and for each v^- reset its peculiar successor succ(v^-) to v⁺.
Goto step 3.

The complexity of this algorithm is about O(n.d^-) with n the number of vertices in the graph and d^- the maximum size of the pred lists. So it may even be linear if, for instance, the graph is a mere circuit.

One may remark that finding the common vertex of the system graph circuits is an instance of the problem of the minimum cutset of size less or equal to k (i.e. the instance with k=1). So any one of the algorithms for finding minimal cutsets which find every cutset with size 1 are suitable for variable elimination. That excludes algorithm D of Shamir, but the one described in [9] is perfect. Indeed, it works for cutsets of size 1 and it finds minimal cutsets for a number of graph classes. This last property is important since even if an elimination is partial there is profit: one obtains a system with less variables. A system with few variables can be analyzed faster by the later phases of the automatic parallelization process (e.g. the scheduling).

Note that a better variable elimination can be achieved using a more precise system graph: the clause graph (whose vertices are clauses and not variables).

The system associated to the program below
DO i=1,2*n
  x(i)=x(2*n-i+1)   (v)
END DO
is
v[i] = case 
        { i | 1<=i<=n }     : x[2*n-i+1] ;
        { i | n+1<=i<=2*n } : v[2*n-i+1] ;
       esac ;
We name the clauses using the name of the variable and their rank in the variable definition. For instance the first clause of v is v.0. If v is included in a strong component, an elimination process may fail because of the loop in the variable graph. In contrast the clause graph does not have this loop, and so the elimination process may go further: