Ordonnancement de récurrences

Chapter 13

Ordonnancement de récurrences

Une fois les scans détectés il faut pouvoir générer un code efficace, c'est-à-dire tenant compte des particularités de ces opérations. Comme notre détecteur est destiné à être inclus dans le paralléliseur PAF, il faut modifier la méthode de parallélisation dite méthode géométrique pour qu'elle exploite le parallélisme implicite des scans et des réductions. La première modification nécessaire concerne le module de calcul des bases de temps. Ce module donne pour chaque opération du programme la date de son exécution. Le calcul classique suppose qu'une opération peut démarrer dès qu'un certain nombre d'autres opérations sont terminées. Une hypothèse implicite du module actuel est que le nombre d'opérations dont dépend une autre opération est constant, c'est-à-dire que ce nombre est un entier positif. Nous allons voir que ce n'est plus le cas lorsque des scans sont explicités dans le système d'équations. Il est alors possible qu'une opération dépende d'un ensemble d'autres opérations. Cet ensemble est un polyèdre convexe défini à l'aide des paramètres de structure.

13.1

Calcul classique de bases de temps

Les données d'un problème d'ordonnancement sont un ensemble d'opérations G et un ordre partiel < sur G. L'ordre partiel représente les dépendances entre les opérations. Ainsi si o₁< o₂ alors l'opération o₂ ne peut pas commencer avant la fin de l'opération o₁, cette contrainte est généralement appelée la contrainte de causalité. Construire un programme parallèle pour les opérations de G consiste à trouver un second ordre partiel <', au moins aussi contraignant que < et s'exprimant facilement sur une machine parallèle. Le problème n'est pas aussi simple qu'il y parait car un programme ne définit pas un seul ensemble d'opérations mais une famille de tels ensembles. Cette famille est indexée par les paramètres de structure du programme. L'ordre <' doit donc être un ordre générique. Une manière de décrire l'ordre <' est de calculer la date d'exécution de chaque opération. L'ensemble de ces dates est appelé une base de temps pour G. La notion de base de temps est apparue d'abord dans le domaine de la conception automatique de circuits systoliques [50]. Ce n'est que récemment qu'elle a été utilisée dans le domaine de la parallélisation automatique [48, 52]. Les bases de temps peuvent être utilisées pour une parallélisation à gros grain. L'idée est de regrouper les opérations en tâches et d'ordonnancer ces tâches. Cette méthode présente quelques inconvénients :

il faut choisir un découpage en tâches maximisant le parallélisme ; ce n'est pas un problème facile ;
il faut connaître la durée d'exécution de ces tâches ; c'est d'autant plus difficile que cette durée dépend généralement des paramètres de structure du programme ;
enfin, une fois le problème posé il reste à le résoudre. Or le problème de l'ordonnancement dans le cas général est NP-complet.

La parallélisation à grain fin, au niveau des opérations, permet de lever une partie de ces inconvénients. Comme le nombre d'opérations est très élevé, il est moins important de connaître leurs durées exactes. Il est même possible de prendre une durée égale à 1. Dans ce cas, le programme parallèle obtenu est encore proche de l'optimal pourvu qu'il comporte un assez grand nombre d'opérations (cf [26]). Par contre il n'est plus possible de trouver un ordonnancement purement numérique. L'analyse du programme ne peut plus s'appuyer sur un graphe des dépendances détaillé, il est nécessaire de travailler à partir d'une structure plus condensée. Le graphe du flot des données (GFD) est un bon candidat ; son principal avantage est qu'il décrit de façon exacte la classe des programmes statiques avec des fonctions d'indices linéaires. Les dates d'exécution des opérations doivent être génériques (i.e. des fonctions avec comme domaines de définition des sous-ensembles de G).

Formalisons les contraintes de causalité pour une équation e d'un système d'équations S :

" zÎ D_e, v_e(z)=Exp_e(z) .

Comme indiqué dans la section 7.1.2, les (v_e)_{eÎ S} sont les variables définies par le système S. Les domaines D_e sont des polyèdres. Enfin les Exp_e sont des fonctions conditionnelles. Au niveau d'une clause c de e de domaine de définition D_e^c, l'expression Exp_e(z) s'écrit sous la forme :

" zÎ D_e^c, v_e(z)=Exp

_e^c(v

e₁

(I₁(z)), ...,v

e_n

(I_n(z))) .

Les (I_k)_kÎ{1,...,n} sont des fonctions d'indices linéaires. Pour cette clause c, les contraintes de causalité s'écrivent :

" kÎN_n^*, " zÎ D_e^c, q(e,z) ³ q(e_k, I_k(z)) + 1 (13.1)

Il y a donc autant de séries de contraintes de causalité que de clauses dans le membre droit de l'équation e. L'ensemble des contraintes de causalité forme un système d'inéquations. Il est impossible de résoudre ce système pour une base de temps q quelconque. Aussi toutes les méthodes imposent a priori la forme des bases de temps. Plus cette forme est générale, plus la méthode est efficace. À notre connaissance la méthode calculant les bases de temps les plus générales est présentée dans [28, 29]. Une fois la fonction q remplacée par sa forme générale, le système d'inéquations est résolu en minimisant une fonction de coût (e.g. la durée totale du programme parallèle). La méthode utilisée dans [28] pour résoudre le système est particulièrement efficace puisqu'il se ramène à la minimisation d'une fonction linéaire sous des contraintes elles aussi linéaires. La linéarisation du système d'inéquations initial est effectuée en utilisant le lemme de Farkas.

Pour une base de temps donnée q, l'ensemble des opérations à exécuter à la date t (noté F(t)) est appelée un front. Si un ensemble d'opérations est assimilé aux valeurs qu'il calcule, il vient :

F(t)={ v_e(z) | q(e,z)=t } .

13.2

Modèle de machine parallèle

Dans le cadre de la parallélisation automatique les bases de temps donnent les dates d'exécution des opérations d'un programme sur une machine parallèle. En fait lors du calcul des suppositions sont faites sur l'architecture de la machine parallèle. Le modèle ciblé est une machine à mémoire partagée avec un nombre illimité de processeurs (ce type de machine est connu dans la littérature sous le nom de para-ordinateur [57]). Ainsi quel que soit son nombre d'opérations, un front peut s'exécuter en un cycle. La résolution du système est plus facile. Un tel programme peut toujours être exécuté sur une machine réelle (donc avec un nombre limité de processeurs) en utilisant des processeurs virtuels et une boucle de virtualisation. La plupart des langages parallèles disposent de boucles DO ALL qui gèrent la virtualisation. Dans le cas du calcul de bases de temps en présence de réductions ou de scans une autre supposition doit être faite. 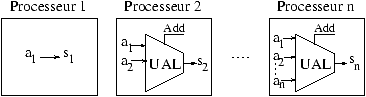Cette supposition est que chaque processeur de la machine cible doit avoir une unité arithmétique et logique (UAL) avec un nombre illimité d'entrées. Dans ces conditions les réductions et les scans les plus communs peuvent être exécutés en un temps constant (i.e. ne dépendant pas de la taille des données à traiter).

Sur une telle machine, le scan classique :
scan(+,[a₁,...,a_n]) ,
qui calcule les sommes partielles des éléments d'un tableau, peut être exécuté en un cycle (voir le schéma ci-dessous).

Évidement, une base de temps calculée pour une machine avec un nombre illimité de processeurs et avec des UAL dont le nombre d'entrées n'est pas borné doit être adaptée pour être utilisée sur une machine réelle. Le squelette du programme parallèle associé à la base de temps est :

DO t=0,L
 Exécute toutes les opérations du front F(t)
END DO

Prenons d'abord en compte le fait que la machine réelle ne possède pas un nombre illimité de processeurs. La boucle de virtualisation pour une machine à p processeurs peut s'écrire comme suit.

DO t=0,L
 ops=F(t)
 DO WHILE ops n'est pas vide
   Exécute simultanément p opérations de ops
   Retirer ces opérations de ops
 END DO
END DO

Il faut ensuite prendre en compte le fait que la machine cible n'a pas d'UAL avec un nombre illimité d'entrées. La méthode la plus efficace (en théorie) pour effectuer une réduction ou un scan est d'utiliser un arbre binaire de calcul. Pour une opération portant sur n éléments, il est nécessaire d'allouer n processeurs. Pour implanter cette méthode sur une machine réelle, il faut donc utiliser une autre boucle de virtualisation (plus complexe que la précédente). Or certaines machines parallèles n'implantent pas de boucle de virtualisation de façon efficace. Ainsi celle de la CM-2 de TMC itère tous les processeurs virtuels qu'ils aient une opération à effectuer ou non. Dans le cas de la réduction, le calcul par arbre binaire nécessite n/2 processeurs virtuels pour la première étape. Donc, sur une machine avec une boucle de virtualisation non optimisée, et bien que cela soit inutile, n/2 processeurs virtuels sont aussi itérés pour les log₂(n/2) autres étapes. Si la machine dispose de p processeurs, le temps d'exécution du calcul est de l'ordre de log₂(n)n/2p. Si la boucle de virtualisation est implantée efficacement, n/2 calculs sont nécessaires pour la première étape, n/4 pour la seconde et ainsi de suite. Si n est grand le temps de calcul est donc de l'ordre de n/p, car la suite de terme général 1+1/2+1/4+...+ 1/2ⁿ tend vers 2 quand n tend vers l'infini. Ces temps sont à comparer avec celui d'une variante du calcul par arbre binaire, la méthode dite du partitionnement. Cette variante consiste à découper le vecteur des données en sous-vecteurs (chaque sous-vecteur sera associé à un processeur). Chaque processeur effectue l'opération sur ses données propres. Enfin les résultats partiels sont propagés et les processeurs mettent à jour leurs données. Les première et dernière étapes s'exécutent en un temps de l'ordre de n/p, l'étape intermédiaire en un temps de l'ordre de log₂(p). En conclusion, la méthode par arbre binaire n'est envisageable que si la boucle de virtualisation est implantée efficacement. Sinon le rapport des temps entre la méthode par l'arbre de calcul et celle par partitionnement est, si n est grand, de l'ordre de log₂(n/2)/2. Il est donc préférable d'employer la méthode du partitionnement.

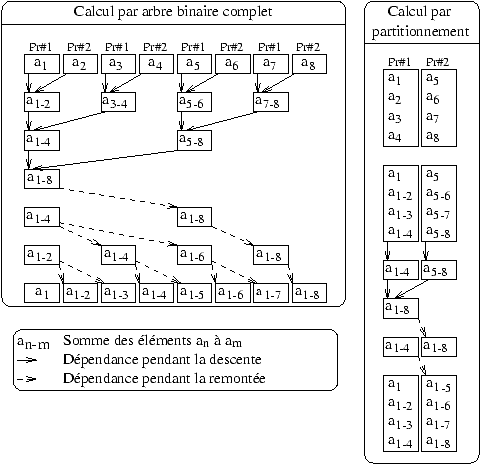
Considérons le scan ci-dessous.

scan (+,[a₁,a₂,a₃,a₄,a₅,a₆,a₇,a₈]) .

Avec nos notations ce scan s'écrit :
Scan( { i' | 0 <= i' <= 8 }, +, ( [1] ), a[i'], 0 )
La différence entre la méthode de l'arbre binaire de calcul et la méthode du partitionnement, pour une machine avec deux processeurs pr#1 et pr#2, est illustrée sur le dessin ci-dessous.

13.3

Ordonnancer des réductions et des scans

Pour ordonnancer des scans et des réductions exprimés avec l'opérateur Scan, des modifications doivent être apportées aux algorithmes de [28, 29]. La principale modification à apporter concerne l'algorithme de génération des conditions de causalité. Considérons un opérateur Scan quelconque :

Scan( D

,(e_i)

iÎ{1,...,k}

,b,d,g) .

Cet opérateur calcule les valeurs d'un tableau multi-dimensionnel v. Pour chaque élément z du domaine de définition D, nous notons P(z) l'ensemble :

{ z'Î D

| z' <

e₁,...,e_k

z } .

La relation d'ordre <_e_₁_,...,e_{_k}^D utilisée dans cette expression est définie ci-dessous.

" z,z' Î D× D

, z <

e₁,...,e_k

$ (l₁,...,l_k) Î Z

^k, l» 0, z+

i=1

l_i.e_i=z'

Intuitivement cet ensemble contient les points de D associés aux données, les (d(z')), nécessaires au calcul de la valeur v(z). Le plus petit point I(z) de cet ensemble est particulier puisqu'il n'est pas associé à une donnée mais à une valeur initiale g( I(z)). Ce point peut être calculé directement par la formule :

I(z)=min

e₁,...,e_k

(z) .

L'ensemble des points de P(z) moins le point I(z) est noté P(z). De la même façon l'ensemble des points de D ne correspondant pas à une valeur d'initialisation est noté D. L'ensemble D peut être obtenu par la formule générale :

D= D-min

e₁,...,e_k

( D) .

Dans le cas des scans uni-directionnels, l'expression se simplifie en :

D= DÇ( D+e₁) .

Dans ce contexte les contraintes de causalité pour l'opérateur Scan sont :

" zÎ D, " z'Î P(z), q(v,z)³ q(d,z') + 1 ,

" zÎ D, q(v,z)³ q(g, I(z)) + 1 .

Les fonctions q(d,.) et q(g,.) donnent les temps auxquels les données et les valeurs d'initialisation du scan sont prêts. De ce fait les contraintes de causalité donnent lieu à une inégalité par référence à une autre équation (ou clause) dans l'expression d et dans l'équation g. Ces contraintes expriment le fait que, sur une machine avec un nombre illimité de processeurs et avec des UAL possédant un nombre illimité d'entrées, un scan s'exécute en un nombre constant de cycles. L'exécution du scan est déclenchée dès que toutes les données nécessaires au calcul sont prêtes.

Les contraintes de causalité telles que (11.2) ne sont plus de la forme de l'inégalité (11.1). Cependant les méthodes de [28, 29] peuvent être adaptées pourvu que l'ensemble

{ (z,z') | zÎ D, z'Î P(z) } ,

soit convexe. Ces méthodes sont basées sur le lemme de Farkas.

Lemme 10 (lemme de Farkas)
Soit D un polyèdre non vide défini par p inégalités affines :

a_i.x+b_i ³ 0, i=1,p .

Une forme affine y est positive sur D ssi il s'agit d'une combinaison positive des formes affines définissant D :

y(x) º n₀+

i=1

n_i(a_i.x+b_i), n_i³ 0 .

Le problème de l'ordonnancement se résume à la résolution d'un système d'équations linéaires par deux applications du lemme de Farkas. Supposons que l'ensemble d'inégalités

" kÎN

n_v

, F_v,k(z)³ 0 ,

définisse le domaine D. Alors, par le lemme de Farkas et puisque la fonction q(v,.) est positive sur D, il vient :

$ (µ_k)

kÎ N

n_v

, " kÎ N

n_v

, µ_k³ 0 et

q(v,z) º µ₀+

n_v

k=1

µ_k F_v,k(z) .

De même, supposons que l'ensemble d'inégalités

" kÎ N

n_p

, Y_p,k(z,z')³ 0 ,

définisse l'ensemble décrit par (11.3). Toujours le même lemme de Farkas permet d'écrire que :

$ (l_k)

kÎ N

n_p

, " kÎ N

n_p

, l_k³ 0 et

q(v,z)-q(d,z')-1 º l₀+

n_p

k=1

l_k Y_p,k(z,z') .

Il s'agit d'une identité dans laquelle les coefficients des mêmes variables peuvent être égalisés. Le système résultant, qui est un ensemble d'équations en les l_k et en les µ_k, définit l'ensemble des bases de temps valides. Une base de temps particulière peut alors être choisie suivant un critère d'optimalité, comme la minimisation de la latence ou la minimisation des délais. Le lecteur est renvoyé à [28] pour de plus amples détails.

La difficulté de l'ordonnancement des opérateurs Scan réside dans le calcul de l'ensemble P(z) et du point I(z). Il est à noter que tous les sur-ensembles de P(z) et de { I(z)} conduisent à des ordonnancements valides. Simplement, ces ordonnancements ne sont pas optimaux. La plus simple des approximations est de prendre D pour P(z) et min_e_₁_,...,e_{_k}^D( D) ¹ pour { I(z)}. La condition de causalité est alors :

" zÎ D, " z'Î D, q(v,z)³ q(d,z) + 1 ,

" zÎ D, " z'Î min

e₁,...,e_k

( D), q(v,z)³q(g,z') + 1 .

Ces conditions sont assez simples à obtenir, mais il est possible de faire mieux. Deux cas sont à envisager, les opérateurs Scan uni-directionnels et les opérateurs Scan multi-directionnels. Dans le cas de scans uni-directionnels les coordonnées génériques du point I(z) sont données par la résolution du problème en nombres entiers :

b=max{a | a Î N, z-a e₁Î D} .

C'est le genre de problème que résoud très bien le logiciel PIP. L'expression des coordonnées du point I(z) est alors z-b e₁. Du coup, l'ensemble P(z) s'exprime simplement :

P(z)={z-l e₁ | lÎN

b-1

} .

Considérons maintenant le cas général des scans multi-directionnels. Le point I(z) peut toujours être calculé par PIP. En effet ce logiciel est capable de calculer des maximums lexicographiques. Le problème à résoudre s'écrit :

b=lexmax{a | a Î N

^k, z-

i=1

a_i e_i Î D} .

L'ensemble P(z) peut être calculé, lui aussi, à partir de b :

P(z)={ z'Î D

| z'=z-

i=1

a_i e_i, 0

a«b } .

Cet ensemble n'est pas forcément convexe mais c'est l'union d'ensembles convexes. Notons 0«_i a le prédicat

Ù_i'=0^i-1 (a_i'=0) Ù (a_i>0) ,

et a«_j b le prédicat

Ù_j'=0^j-1 (a_j'=b_j') Ù (a_j>b_j) .

L'ensemble P(z) est égal à :

iÎN_k+1, jÎN_k

{ z'Î D

| z'=z-

i=1

a_i e_i, 0

_i aÙ a«_j b } ,

(a_k+1 est fixé à 1). C'est donc bien l'union de k(k+1) ensembles convexes. La condition de causalité est éclatée en plusieurs ensembles d'inégalités. Il faut noter que k est toujours très petit (les scans multi-directionnels courants ne comportent que 2 ou 3 directions).

Une transformation est toujours appliquée au tableau de valeurs calculé par un scan. L'expression d'une clause c comportant un opérateur Scan est de la forme :

" zÎ D_c, v_c(z)= ...Scan( D,P,b,d,g)(f(z))... .

Cela signifie qu'il n'est pas nécessaire de trouver la base de temps de toutes les valeurs calculées par l'opérateur. Il suffit de prendre en compte uniquement les valeurs accédées au travers de la transformation f. Dans cette optique, la condition de causalité doit être légèrement corrigée :

" zÎ f( D_c), " z'Î P(z), q(v,z)³ q(d,z') + 1 ,

" zÎ f( D_c), q(v,z)³ q(g, I(z)) + 1 .

Cette condition est moins contraignante (si f( D_c) est strictement inclus dans D) que la condition (11.2). Il y a donc un espoir d'obtenir de meilleures base des temps (e.g. avec une latence plus faible). Nous insistons sur le fait qu'une base de temps par opérateur Scan est calculée. Il serait possible de ne calculer que la base de temps pour la clause c mais les bases de temps intermédiaires des opérateurs Scan sont nécessaires à la génération de code.

L'ordonnancement des systèmes d'équations contentant des scans explicites est résumé dans l'algorithme suivant :

Algorithme 11 Ordonnancement des systèmes avec scans explicites

Générer les contraintes de causalité :
- Générer les contraintes classiques (11.1) en faisant abstraction des opérateurs Scan.
- Générer les contraintes liées aux scans (11.2).
Construire le graphe mettant en relief les contraintes entre les différentes bases de temps (les sommets sont les fonctions de base de temps, un arc existe entre deux fonctions si une contrainte de causalité les lie).
Calculer les composantes fortement connexes de ce graphe.
Pour chaque composante fortement connexe (énumérées par un tri topologique) ;
1. Regrouper les contraintes de causalité concernant les fonctions de base de temps de la composante.
2. Appliquer Farkas sur les contraintes ;
3. Résoudre le système d'équations en optimisant un critère tel que la latence maximale.

La décomposition en composantes fortement connexes a pour but de minimiser la taille des systèmes d'équations à résoudre. En effet le temps de résolution croît très rapidement avec le nombre d'équations. Il est plus efficace de résoudre plusieurs petits systèmes, qu'un seul de plus grande taille. Cette décomposition est valide dans la mesure où les composantes fortement connexes sont connectées par un graphe sans circuit. Il faut d'abord trouver les solutions des fonctions correspondant à des composantes sans prédécesseur, puis les solutions des fonctions correspondant aux composantes sans prédécesseur non déjà traité et ainsi de suite. L'ordre est donné par le tri topologique du graphe.

13.4

Un exemple d'ordonnancement de scan

Prenons un exemple pour illustrer la génération des conditions de causalité et la résolution du système correspondant. Le programme

DO i=1,n
 DO j=1,m
  a(i,j)=a(i,j-1)+a(i,j)  (v1)
 END DO
END DO

calcule un ensemble de n scans traitant chacun m données. Voici un extrait du système final, après la détection des récurrences :

x1 : { i,j | 1<=i<=n, 1<=j<=m } of real ;
x2 : { i,j | 1<=i<=n, 1<=j<=m } of real ;
v1 : { i,j | 1<=i<=n, 1<=j<=m } of real ;

v1[i] = Scan( { i',j' | 1<=i'<=n, 0<=j'<=m }, ([0 1]),
              +, x1[i',j'], x2[i',j'] )[i,j] ;

Les symboles x1 et x2 représentent les équations qui initialisent le tableau a. Nous supposons que les bases de temps de ces équations sont connues :

q(x1,(i,j))=0 et q(x2,(i,j))=m-j+i .

Nous sommes en présence d'un opérateur uni-directionnel, pour trouver le point d'initialisation I(i,j), il faut d'abord calculer :

b=max{a | a Î N,

æ
è

ö
ø

-a

æ
è

ö
ø

Î N_n^*×N_m} .

la solution est b=j. Le point d'initialisation est donc

I(i,j)=

æ
è

ö
ø

et l'ensemble P(i,j) s'en déduit :

P(i,j)=

ì
í
î

æ
è

ö
ø

| lÎN_j^*

ü
ý
þ

Enfin le domaine D est l'intersection de N_n^*× N_m avec son translaté de vecteur (0,-1). C'est à dire N_n^*× N_mÇN_n^*× N_m+1^*= N_n^*× N_m^*. Puisque f est l'identité, la condition de causalité s'écrit :

" (i,j)Î N_n^*× N_m^*, " j'Î N_j^*, q(v,(i,j))³ q(x1,(i,j')) + 1 ,

" (i,j)Î N_n^*× N_m^*, q(v,(i,j))³ q(x2,(i,0)) + 1 .

En reportant les bases de temps de x1 et x2 dans la condition, il vient :

" (i,j)Î N_n^*× N_m^*, " j'Î N_j^*, q(v,(i,j))³ m - j' + i + 1 ,

" (i,j)Î N_n^*× N_m^*, q(v,(i,j))³ 1 .

La base de temps de x1 se devant d'être positive la seconde inégalité de la condition de causalité est toujours vérifié. Reste la première inégalité. Comme q(v,.) doit être, elle aussi positive, Farkas assure qu'il existe des µ_i positifs tels que :

" (i,j)Î N_n^*× N_m^*,

q(v,(i,j))=µ₀+µ₁(i-1)+µ₂(n-i)+µ₃(j-1)+µ₄(m-j) .

Farkas est à nouveau appliqué, à la condition de causalité cette fois :

µ₀+µ₁(i-1)	+µ₂(n-i)+µ₃(j-1)
	+µ₄(m-j)-(m-j'+i)-1
º
l₀+l₁(i-1)	+l₂(n-i)+l₃(j-1)+l₄(m-j)
	+l₅(j'-1)+l₆(j-j') .

Le système à résoudre pour trouver l'ensemble des bases de temps valides est :

µ₁-µ₂	=	l₁ - l₂ + 1
µ₃-µ₄	=	l₃ - l₄ + l₆
0	=	l₅ - l₆ - 1
µ₂	=	l₂
µ₄	=	l₄ + 1
µ₀-µ₁-µ₃	=	l₀-l₁-l₃-l₅+1 .

Il reste à choisir un critère d'optimisation. Le plus simple, pour une résolution ``à la main'', est de minimiser les µ_i. Le résultat sera une base de temps avec de petits coefficients, donc avec une faible latence. Simplifions d'abord le système :

µ₁	=	l₁ + 1
µ₃	=	l₃ + l₆ + 1
0	=	l₅ - l₆ - 1
µ₂	=	l₂
µ₄	=	l₄ + 1
µ₀	=	l₀ + l₆ - l₅ + 3 .

Les contraintes sur les µ_i sont :

µ₀³ 0, µ₁³ 1, µ₂³ 0, µ₃³ 1, µ₄³ 1 .

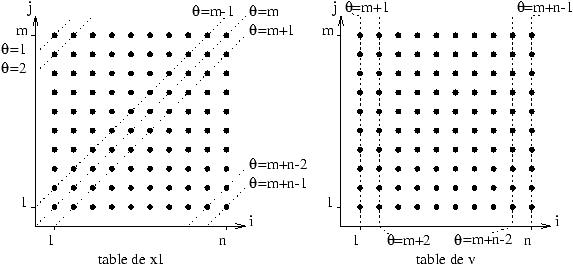
Une solution pour la base de temps de l'opérateur Scan est donc q(v,(i,j))=i+m. C'est d'ailleurs la solution intuitive, comme le montre les cartes des base de temps de x1 et de v :

13.5

Effets de bords de la détection de scans

La détection des scans puis leur ordonnancement par une méthode adaptée a un avantage direct : le parallélisme lié aux scans est exploité. Mais cette méthode présente d'autres avantages plus inattendus. En effet elle peut conduire à accélérer le calcul de la base de temps ou à trouver un meilleur ordonnancement.

Lors de la normalisation des graphes, le détecteur de scans a tendance à concentrer les composantes fortement connexes du système d'équations sur une seule équation. Ce n'est pas toujours possible mais des équations sont généralement supprimées (car elles deviennent inutiles). En conséquence le nombre de sommets dans le graphe du flot des données du système final est généralement inférieur à celui du GFD du système initial. L'ordonnancement du système final prend alors moins de temps que celui du programme source. Il se trouve même des cas où la somme des temps de détection des scans et d'ordonnancement du système d'équations est inférieur au temps de l'ordonnancement classique. Cela arrive lorsque le GFD du programme source comporte de grandes composantes fortement connexes et que le détecteur de récurrence diminue la taille de ces composantes. En effet le calcul d'une base de temps consiste à résoudre des systèmes linéaires dont la taille est proportionnelle à celle des composantes fortement connexes. Le temps d'exécution du module d'ordonnancement croît donc rapidement en fonction de cette taille.

Nous avons fait quelques test avec des programmes de la forme :
DO i=1,n
 a1(i)=f1(c1(i-1))      (v1)
 a2(i)=f2(c1(i-1))      (v2)
 a3(i)=f3(c1(i-1))      (v3)
 a4(i)=f4(c1(i-1))      (v4)
 b1(i)=g1(a1(i),a2(i))  (v5)
 b2(i)=g2(a3(i),a4(i))  (v6)
 c1(i)=h1(b1(i)+b2(i))  (v7)
END DO
Le détecteur de récurrences réduit ce programme à une seule équation. Donc l'ordonnancement du système se fait pour une composante fortement connexe réduite à un sommet au lieu d'une composante constituée de 7 sommets. Ce programme possède 3 niveaux de variables intermédiaires, les tests ont aussi été faits pour 4, 5 et 6 niveaux de variables. Le tableau ci-dessous donne les temps d'exécution pour ordonnancer directement le programme et celui pour d'abord détecter les récurrences puis ensuite les ordonnancer.

Niveau Ordonnancement seul Détection puis ordonnancement Accélération

3 31s 34s+2s 0.9

4 310s 71s+2s 4.2

5 3608s 180s+2s 19.8

6 46779s 471s+2s 99.1

Les tests ont été effectués sur une SparcStation SLC, il s'agit donc d'une station de bas de gamme. De plus, les programmes Lisp étaient interprétés et non compilés (la pseudo-compilation apporte une accélération supérieure à 2).

Un autre effet de bord est l'amélioration de l'ordonnancement de programmes ne contenant pas de récurrences. Cela n'est vrai que lorsque le détecteur utilise le graphe des clauses. Ce graphe ne permet pas seulement une plus grande précision dans la détection mais aussi l'amélioration de la base de temps (en terme de latence ou de délais). L'amélioration vient du fait qu'une fonction est associée à chaque clause, plutôt qu'à chaque équation comme dans l'ordonnancement classique.

Un ordonnancement direct de la boucle
x(0)=0             (v1)
DO i=1,2*n
  x(i)=x(2*n-i+1)  (v2)
END DO
donne les bases de temps suivantes pour v1 et v2 :
q(v1)=0 et " iÎN_2n^*, q(v2,i)=i-1 .
Le détecteur de récurrences transforme le programme source en une équation à deux clauses :
x  : { i | 1 <= i < 2*n }  of real ;
v2 : { i | 1 <= i < 2*n }  of real ;
v2[i] = case
         { i | 1 <= i <= n }     : x[2*n-i+1] ;
         { i | n+1 <= i <= 2*n } : v2[2*n-i+1] ;
        esac ;
L'ordonnancement clause par clause donne des bases de temps triviales :
" i, 1£ i£ n, q(v2.0,i)=0 et " i, n+1£ i£ 2n, q(v2.1,i)=1 .

Il est certain que l'ordonnancement clause par clause est plus précis que l'ordonnancement équation par équation mais il faut bien voir que cela demande un plus grand nombre de résolution de systèmes. Ce n'est pas, non plus, la panacée en terme d'efficacité ; l'ordonnancement obtenu n'est pas le meilleur ordonnancement affine par morceaux. Il s'en rapproche, c'est tout. C'est cependant un bon compromis entre l'ordonnancement équation par équation et un ordonnancement découpant aléatoirement le domaine de définition des équations pour y affecter une fonction de base de temps. Le découpage clause par clause a l'avantage de respecter la sémantique du système d'équations.

1: Attention cet ensemble n'est pas un convexe dans le cas général, il doit être décomposé pour que le lemme de Farkas soit applicable.

Niveau	Ordonnancement seul	Détection puis ordonnancement	Accélération
3	31s	34s+2s	0.9
4	310s	71s+2s	4.2
5	3608s	180s+2s	19.8
6	46779s	471s+2s	99.1