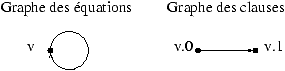| Chapter 8 |
Présentation de la méthode des systèmes d'équations |
|
Ce chapitre formalise la notion de système d'équations puis
expose le schéma général de notre méthode de détection.
En fait, plusieurs schémas différents sont envisagés. Les
plus simples présentent l'avantage de la rapidité d'exécution
et les plus précis présentent l'avantage d'une plus grande
efficacité. Enfin l'outil de base de la normalisation, la
substitution dans un système d'équations, est présenté.
Nous verrons, là aussi, qu'il faut choisir entre la rapidité
d'exécution et la précision de la substitution.
| 8.1 |
Mise sous forme de systèmes d'équations |
|
Dans le cadre du projet PAF les programmes sources sont écrits dans
un sous-ensemble à contrôle statique de Fortran 77.
La première étape de notre détecteur est de transformer
ces programmes en des systèmes d'équations récurrentes.
Cela peut être réalisé en passant les programmes Fortran
en assignation unique. Il est aussi montré que la transformation
peut être effectuée en présence d'instructions conditionnelles.
| 8.1.1 |
Passage en assignation unique |
|
Pour traduire le programme source en un SER nous utilisons
l'algorithme présenté dans [27] qui calcule
son Graphe du Flot des Données (GFD). Rappelons que le GFD donne pour
chaque opération du programme les opérations ayant calculé les
valeurs qu'elle utilise.
Une opération est un couple formé d'une instruction et d'un vecteur
d'itération. Chaque instruction du programme génère donc autant
d'opérations que le nid de boucle l'englobant génère d'itérations.
Les arcs du GFD indiquent qu'un sous-ensemble des opérations constituant
l'instruction cible ont comme sources un sous-ensemble des opérations
constituant l'instruction destination.
Avec ce GFD il est aisé de traduire le programme initial en un programme
à assignation unique, c'est-à-dire un programme dans lequel une variable
scalaire ou un élément de tableau n'est écrit qu'une seule fois.
Pour cela il suffit de renommer et d'expanser les variables du programme
source. Le lien entre les nouvelles variables est donné par le GFD.
Prenons comme exemple le programme ci-dessous.
x(0)=0 (v1)
DO i=1,2*n
save=x(2*n-i+1) (v2)
x(i)=x(i-1)+save (v3)
END DO
Le GFD de ce programme est résumé par :
Source de x(2*n-i+1) dans v2 ;
* IF [ (i-n-1>=0) ] -> (v3,2*n-i+1)
Source de x(i-1) dans v3 ;
* IF [ (-i+1>=0) ] -> (v1)
* IF [ (i-2>=0) ] -> (v3,i-1)
Source de save dans v3 ;
* (v2,i)
la variable save est expansée en v2(i), c'est-à-dire
qu'elle est renommée suivant le label de l'instruction et expansée
avec le compte-tour de la seule boucle qui l'englobe.
Les autres membres gauches sont expansés suivant le même principe.
Les références aux variables initiales dans les membres droits
sont alors remplacées par leurs sources. Par exemple,
la référence à x(i-1) dans l'instruction v3 est
remplacée par une référence à v1 pour la première
itération et à elle-même pour les autres itérations.
Il est possible d'exprimer le programme en assignation unique dans un
dialecte Fortran incluant des expressions conditionnelles :
v1=0
DO i=1,n
v2(i)=IF (i.GE.n+1) THEN
v3(2*n-i+1)
ELSE
x(2*n-i+1)
END IF
v3(i)=IF (i.LE.1) THEN
v1+v2(i)
ELSE IF (i.GE.2) THEN
v3(i-1)+v2(i)
END IF
END DO
Quand aucune source n'est trouvée pour une référence, c'est que
la variable correspondante n'a pas été initialisée dans la portion
de programme analysé. La variable initiale est alors laissée telle
quelle (e.g. x(2*n-i+1) dans le texte de v2(i)).
Pour les prototypes nous avons utilisé le module de calcul du GFD du
projet PAF. Ce module fonctionne avec en entrée des programmes
à contrôle statique et avec des fonctions d'indices affines.
| 8.1.2 |
Système d'équations |
|
Un programme en assignation unique est équivalent à un
système d'équations récurrentes. Comme le GFD impose que
les fonctions d'accès soient affines il s'agit même d'un
système d'équations affines récurrentes (SERA).
Chaque équation d'un tel système S peut s'écrire sous la
forme :
|
|
zÎ De, ve(z)=Exp |
e(v |
|
(I1(z)),
...,v |
|
(In(z))) . |
|
|
Expe(z)= |
ì
ï
í
ï
î |
| Expe1(z) |
if zÎ De1 |
·
·
· |
| Expem(z) |
if zÎ Dem |
|
|
Des langages tel que le langage Alpha ([45]) permettent
de décrire de tels systèmes d'équations. Dans le langage Alpha,
l'objet de base est la variable spatiale. C'est à dire un triplet
< D,f,V> où la fonction f associe à chaque point entier
du convexe D une valeur de l'ensemble V, l'ensemble V pouvant
être l'ensemble des booléens, des entiers, des réels, etc.
Bien que les systèmes SERA que manipulent nos prototypes ne soient pas
écrits en Alpha (ce langage se prête mal à une représentation
lispienne), tous les exemples que nous donnerons seront en Alpha.
Une équation générique d'un SERA s'écrit en Alpha :
z : { i, j,... | bb <= i <= bh, ... } of <type>
z = case
{ i, j,... | bb1 <= i <= bh1, ... } : exp1 ;
...
{ i, j,... | bbm <= i <= bhm, ... } : expm ;
esac ;
Le mot clef <type> décrit le type des scalaires associés aux
points de l'ensemble z. En Alpha, les domaines convexes
sont exprimés par les inégalités les définissant.
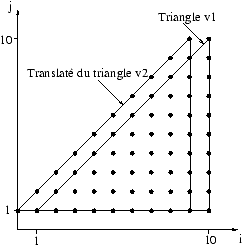
Par exemple, le triangle de ce schéma
se représente par
{ i,j | 1 <= i <= 10, 1 <= j <= i }
Ainsi, la première clause du SERA décrit en Alpha comporte
la définition d'un convexe à l'aide d'inégalités :
{ i, j,... | bb1 <= i <= bh1, ... }
Ce convexe correspond à De1 dans l'écriture classique
(7.1) du SERA. Il en est de même pour les autres clauses.
Les expressions Alpha ne sont pas les expressions classiques
des langages impératifs. Les opérateurs (dits immobiles)
d'Alpha portent directement sur les variables spatiales
et non pas sur les scalaires un à un.
Le petit système Alpha suivant
v1 : { i,j | 1 <= i <= 10, 1 <= j <= i } of real ;
v2 : { i,j | 1 <= i <= 10, 1 <= j <= i } of real ;
v1 = v1 + v2 ;
additionne les valeurs correspondantes (géométriquement parlant)
des triangles v1 et v2. Les résultats sont associés
aux points de v1.
Il est donc nécessaire de définir un opérateur de changement
de base pour décrire des expressions un peu plus complexes.
Cet opérateur est le point (le caractère '.'). La transformation
du changement de base est exprimée à partir des indices de définition
de la variable spatiale.
Considérons le système Alpha ci-dessous.
v1 : { i,j | 1 <= i <= 10, 1 <= j <= i } of real ;
v2 : { i,j | 1 <= i <= 10, 1 <= j <= i } of real ;
v1 = v1 + v2 . (i,j -> i+1,j) ;
Chaque valeur associée à un point du triangle v1 est ajoutée
au point du triangle v2 qui se trouve juste à sa droite. Tout se
passe comme si l'opération s'effectuait entre v1 et l'image de
v2 par la translation de vecteur -i (voir le schéma
ci-dessous).
La somme n'est bien sûr définie que sur l'intersection des deux
triangles.
Une notation plus commode peut être employée lorsqu'il n'y a pas
d'ambiguïté sur les indices utilisés. Il s'agit d'une notation
tableau à la Fortran. C'est cette notation que nous utiliserons pour
nos exemples.
L'exemple précédent peut s'écrire plus simplement :
v1 : { i,j | 1 <= i <= 10, 1 <= j <= i } of real ;
v2 : { i,j | 1 <= i <= 10, 1 <= j <= i } of real ;
v1[i,j] = v1[i,j] + v2[i+1,j] ;
Un système Alpha présente alors une forte analogie
avec un programme Fortran dont les boucles seraient implicites
plutôt qu'explicites.
Les opérations d'un système d'équations, de manière analogue
aux opérations d'un programme, sont représentées par des couples
(e,z) où e est une équation du système S et z un
point de son domaine de définition.
Comme les systèmes d'équations que nous manipulons sont construits
à partir de programmes séquentiels impératifs, ils possèdent un
ordre total < sur l'exécution des opérations.
Cet ordre est défini à partir d'un autre ordre < sur les
équations et d'une matrice N (Le symbole « représente l'ordre
lexicographique strict sur les vecteurs. Nous utiliserons aussi, dans la
suite de cette partie, le symbole « pour désigner l'ordre
lexicographique au sens large) :
|
|
|
| " e,e' Î S, " zÎ De,
" z'Î De' |
| (e,z)<(e',z') Û z[1... Ne,e'] «
z'[1... Ne,e'] Ú
(z[1... Ne,e'] = z'[1... Ne,e'] Ù e< e') |
|
|
-
soit, dans le nid de boucles englobant les deux opérations,
l'itération incluant la première précède l'itération incluant
la seconde ;
- soit, les deux opérations sont dans la même itération
du nid de boucle et la première précède la seconde
dans le texte du programme.
Pour être plus précis, l'inégalité e < e' indique que
l'instruction correspondant à l'équation e précède
l'instruction correspondant à e' dans
le programme initial. La matrice N est une matrice entière symétrique
de taille le nombre d'équations dans le système. Un élément Ne',e
donne le nombre de boucles qui englobent les instructions correspondant aux
équations.
La sémantique de l'ordre < n'a plus de sens au niveau des
systèmes d'équations puisque les boucles disparaissent. Cet ordre reste
cependant important. Par exemple, les références entre équations
respectent cet ordre. Ainsi pour une référence dans une équation
e sur le domaine Dr à une équation e' avec la transformation
affine L, l'inégalité suivante est toujours vérifiée :
|
" zÎ Dr, (e,z) < (e',L(z)) . |
Pour être complet il faut préciser une propriété importante de
la matrice N due à la structure des boucles dans le programme
impératif initial. Si e,e' et e'' sont trois équations telles
que e< e' < e'' alors
|
Ne,e''=min(Ne,e',Ne',e'')
. |
-
Preuve:
-
Ceci est dû au fait que les boucles sont forcément incluses
les unes dans les autres. Donc si on appelle
i,i' et i'' les instructions correspondant aux équations dans
le programme initial, il ne peut pas y avoir à la fois un nid de boucle
englobant i et i' mais pas i'' et un nid de boucle englobant i' et
i'' mais pas i. Donc soit i, soit i'' n'est englobée que par les
boucles qui englobent les trois instructions. Ces boucles sont exactement
celles qui englobent i et i'' d'où le résultat.
| 8.1.3 |
Prise en compte des instructions conditionnelles |
|
Les instructions conditionnelles peuvent facilement être
prise en compte par notre métode. Cela permet de détecter
des scans exprimées avec des if comme un calcul
de maximum. Nous distinguons deux types d'instructions conditionnelles.
Les conditionnelles ``structurelles'' sont des conditionnelles dont
le prédicat est une fonction affine des comptes-tours des boucles
et des paramètres du programme. Les conditionnelles ``sémantiques''
sont les conditionnelles non structurelles.
Les conditionnelles structurelles sont traitées au niveau du calcul
du GFD, par simple insertion du prédicat de la conditionnelle dans
les résultats du module de calcul du GFD. En effet, il suffit de
considérer que le domaine de définition d'une instruction
conditionnelle est l'intersection de son prédicat et
du domaine du nid de boucles dans lequel elle est englobée.
Considérons le code suivant :
s=0 {v1}
DO i=1,n
IF (i.lt.m) THEN k=s+a(i) {v2}
ELSE k=s-a(i) {v3}
END IF
s=k {v4}
END DO
Le prédicat i<m est clairement structurel, le système
d'équations équivalent est donc (dans le cas où m
est compris entre 1 et n) :
a : { i | 1 <= i <= n } of real ;
v1 : real ;
v2 : { i | 1 <= i < m } of real ;
v3 : { i | m <= i <= n } of real ;
v4 : { i | 1 <= i <= n } of real ;
v1 = 0 ;
v2[i] = case
{ i | i = 1 } : v1 + a[i] ;
{ i | i >= 2 } : v4[i-1] + a[i] ;
esac ;
v3[i] = v4[i-1] - a[i] ;
v4[i] = case
{ i | i < m } : v2[i] ;
{ i | i >= m } : v3[i] ;
esac ;
La méthode de détection, présenté dans la suite de cette partie,
peut alors être appliquée. Le résultat de la détection s'écrit,
avec les notations usuelles :
Le prédicat peut même être une combinaison de fonctions
affines par les opérateurs ET, OU et NON logiques. Dans ce
cas il existe un prédicat équivalent en forme normale
disjonctive. L'instruction initiale doit juste être éclatée
pour permettre d'avoir des domaines de définition convexes.
Les conditionnelles sémantiques sont transformées en instructions
gardées. Ainsi une instruction conditionnelle de la forme suivante :
IF predicat THEN
x = expr1
ELSE
y = expr2
END IF
sera transformée en les instructions :
x = IF predicat THEN expr1 ELSE x ENDIF
y = IF predicat THEN y ELSE expr2 ENDIF
Si x et y désignent la même variable il est possible
de fondre les deux instructions en une seule :
x = IF predicat THEN expr1 ELSE expr2 ENDIF
Le cas où les différentes branches de l'alternative comportent plusieurs
instructions se traite de façon analogue.
Cette transformation est à faire avant le calcul du graphe de dépendance.
En effet elle peut faire apparaître de nouvelles références à des
variables (références à x et y si ces variables n'existent
pas déjà dans les expressions expr1 et expr2). La modification
dans le logiciel PAF est moins triviale qu'il n'y parait car il ne faut
transformer ainsi que les instructions conditionnelles sémantiques.
Une transformation uniquement textuelle ne suffit donc pas. Il faut aussi
analyser le programme pour trouver les comptes-tours des boucles et
les paramètres du système. Enfin il faut vérifier que le
prédicat n'est pas affine en ces variables.
Considérons un exemple de calcul de maximum extrait des tests de
l'Argonne ([15]).
j=0 {v1}
DO i = 1,n
IF (b(i).gt.x) THEN
x = b(i) {v2}
j = i {v3}
END IF
END DO
WRITE (*,*) x {v4}
WRITE (*,*) j {v5}
Après transformations le programme devient :
j=0 {v1}
DO i = 1,n
x = IF (b(i).gt.x) THEN b(i) ELSE x ENDIF {v2}
j = IF (b(i).gt.x) THEN i ELSE j ENDIF {v3}
END DO
WRITE (*,*) x {v4}
WRITE (*,*) j {v5}
L'instruction v2 calcule un maximum et l'instruction
v3 l'indice de ce maximum. Nous verrons, dans la
section 10.3, qu'il est possible de détecter ces
deux réductions bien que la fonction binaire et associative
à extraire de l'expression de v3 soit complexe.
| 8.2 |
Schéma général de la détection |
|
Toute méthode de détection de récurrence comporte une étape finale
de reconnaissance de forme pour décider si telle ou telle expression
représente bien une ``bonne'' récurrence (i.e. une réduction ou un scan).
Pour une détection efficace, la reconnaissance doit être appliquée sur
des formes les plus condensées possible, et ce pour deux raisons. La
première est que plus les formes sont condensées, plus le temps
d'exécution de la reconnaissance de formes est réduit. La seconde
raison est que plus les récurrences sont condensées plus la détection
est efficace (i.e. un plus grand nombre de récurrences est détecté).
| 8.2.1 |
Stratégie de normalisation |
|
Nous nous limitons à une reconnaissance de forme sur les expressions
des clauses des équations du système.
Pour que la détection soit tout de même efficace il faut donc que les
récurrences portant sur plusieurs équations soient ramenées
sur une seule. Un outil très utile pour visualiser cette transformation
est le graphe des équations du systèmes. Il est défini comme le graphe
dont les sommets sont les équations du système et les arcs les
références entre les équations. Nous définissons aussi les
sous-systèmes fortement connexes comme étant les sous-systèmes
dont les équations forment une composante fortement connexe dans
le graphe des équations. Dans ce contexte, la
normalisation consiste à contracter les sous-systèmes fortement
connexes sur une seule équation. Plusieurs techniques peuvent
être employées pour arriver à ce résultat.
-
La substitution d'équations : cela revient à supprimer certaines
variables du système en les remplaçant par leur définition (à la
Gauss). Bien entendu ces substitutions ne doivent pas être appliquées
n'importe comment. Le principe est, pour tout sous-système fortement
connexe, de supprimer toutes les variables qui sont
utilisées comme des temporaires. Le cas idéal est celui où le
sous-système se retrouve défini par une seule équation.
- Dans le cas où les substitutions ne suffisent pas, il faut utiliser
le regroupement d'équations. Le regroupement consiste à construire une
équation calculant des vecteurs à partir de quelques équations calculant
des scalaires. Cette méthode permet de détecter des récurrences à
base d'opérations composées comme des opérations sur des complexes
ou sur des matrices de petites tailles.
Après la phase de normalisation, la reconnaissance de
forme peut alors être appliquée aux expressions
des équations qui forment, à elles seules, une composante fortement
connexe. Seules ces équations peuvent être explorées car
la détection d'une récurrence par simple examen d'expression
impose que toutes les références à l'équation elle-même
(les auto-références) soient explicites dans cette expression.
Il ne doit pas y avoir d'auto-référence implicite
(i.e. de circuit sur l'équation qui ne soit pas une boucle).
L'équation v1 dans le système ci-dessous comporte une
auto-référence implicite (il y a un circuit passant par v1
et par v2) :
v1 : { i | 1 <= i < m } of real ;
v2 : { i | 1 <= i < m } of real ;
v1[i] = case
{ i | i = 1 } : 0 ;
{ i | 2 <= i <= n } : v2[i - 1] + a[i] ;
esac ;
v2[i] = case
{ i | i = 1 } : 0 ;
{ i | 2 <= i <= n } : v1[i - 1] + b[i] ;
esac ;
Au vu de l'expression v2[i - 1] on conclut que v1
n'est pas calculée par récurrence. C'est une erreur.
Le système peut être normalisé par le remplacement
de la référence à v2 dans v1 par sa
définition :
v1 : { i | 1 <= i < m } of real ;
v2 : { i | 1 <= i < m } of real ;
v1[i] = case
{ i | i = 1 } : 0 ;
{ i | i = 2 } : 0 ;
{ i | 3 <= i <= n } : v1[i - 2] + b[i - 1] + a[i] ;
esac ;
v2[i] = case
{ i | i = 1 } : 0 ;
{ i | 2 <= i <= n } : v1[i - 1] + b[i] ;
esac ;
La référence dans v1 est maintenant explicite, la récurrence
est détectable par simple examen de l'expression v1[i - 2].
Chaque récurrence détectée est remplacée par une écriture
symbolique de la solution de cette récurrence.
| 8.2.2 |
Raffinement de la normalisation |
|
La principale difficulté (et originalité) de notre travail vient de ce
que nous cherchons des récurrences sur des tableaux multi-dimensionnels.
Les récurrences peuvent être calculées suivant n'importe quelles
directions dans ces tableaux, voire même suivant plusieurs directions
selon un ordre lexicographique (des trajectoires encore plus complexes
peuvent exister, voir section 6.3, mais il est hors de question
de pouvoir en tenir compte). En fait nous sommes amenés, dans la plupart
des cas, à détecter, non pas de simples récurrences, mais des
ensembles de récurrences.
Considérons le programme suivant :
DO i=1,n
DO j=1,n
a(i,j)=a(i-1,j-1)+a(i,j)
END DO
END DO
Ce programme ne calcule pas une récurrence mais un ensemble de
récurrences suivant les diagonales du tableau a.
Il est possible :
-
soit de privilégier la rapidité
d'exécution du détecteur, auquel cas on se limite à la détection
d'ensembles de récurrences calculées suivant une seule direction
(i.e. des récurrences uni-directionnelles) ;
- soit de privilégier la qualité de la détection, c'est-à-dire
détecter aussi les ensembles de récurrences calculées suivant
plusieurs directions (i.e. des récurrences multi-directionnelles).
Dans le premier cas, on peut se contenter de détecter les récurrences
en suivant strictement le schéma général présenté en 7.2.1.
C'est à dire que l'on tente de normaliser le système d'équations en
une seule passe.
L'inconvénient de cette méthode est que la normalisation risque
d'être assez peu efficace.
Le système suivant ne peut pas être normalisé à l'aide
de substitutions (un critère simple pour distinguer les systèmes
normalisables est donné dans la section 8) :
a : { i, j | 1 <= i <= n, 1 <= j <= m } of real ;
b : { i, j | 1 <= i <= n, 1 <= j <= m } of real ;
v1 : { i, j | 1 <= i <= n, 1 <= j <= m } of real ;
v2 : { i, j | 1 <= i <= n, 1 <= j <= m } of real ;
v1[i,j] = case
{ i, j | i = 1, j = 1 } : 0 ;
{ i, j | i >= 2, j = 1 } : v2[i-1,m] ;
{ i, j | j >= 2 } : v1[i,j-1] + a[i,j] ;
esac ;
v2[i,j] = case
{ i, j | j = 1 } : v1[i,m] ;
{ i, j | j >= 2 } : v2[i,j-1] + b[i,j] ;
esac ;
Pourtant, la troisième clause de v1 calcule bien un ensemble
de scans, idem pour la seconde clause de v2. En fait,
la normalisation a échoué parce que les instances de scans
calculées par les deux équations sont inter-dépendantes
(elles ne peuvent pas être calculées en parallèle).
Une méthode de normalisation plus efficace
(que nous appelons normalisation partielle) est de tenir compte de
la structure du programme initial. Les programmes numériques sont
le plus souvent écrits par des humains. Ces programmes ont donc
tendance à être bien structurés. Un premier niveau de structuration
est donné par les procédures et un second par les nids de boucles.
Les problèmes les plus triviaux sont résolus par les boucles les
plus internes (e.g. le calcul d'un produit scalaire), les boucles les
plus externes ont le plus souvent pour but de transmettre les informations
entre les nids de boucles internes.
D'où l'idée de commencer par détecter les récurrences dans les
boucles les plus internes puis dans les boucles juste plus externes et
ainsi de suite. Cela revient à détecter des récurrences pour
un vecteur d'itération des boucles les plus externes fixé.
Avec cette méthode de détection,
les diverses instances d'un ensemble de récurrences peuvent être
inter-dépendantes. Cela compliquera la génération de code pour
ces récurrences.
L'exemple précédent est normalisé, si, dans chaque équation,
i est considéré comme fixé. Le graphe du système comporte alors 2
composantes fortement connexes, v1 et v2. Supposons
que scansum(d,g) représente l'ensemble des scans qui calculent
les séries sum suivantes (indicées par i) :
sum : { j | 1 <= j <= n } of real ;
sum[j] = case
{ j | j = 1 } : g[i, j] ;
{ j | j >= 2 } : sum[i,j-1] + d[i, j] ;
esac
Le système se réécrit alors :
a : { i, j | 1 <= i <= n, 1 <= j <= m } of real ;
b : { i, j | 1 <= i <= n, 1 <= j <= m } of real ;
v1 : { i, j | 1 <= i <= n, 1 <= j <= m } of real ;
v2 : { i, j | 1 <= i <= n, 1 <= j <= m } of real ;
v1[i,j] = case
{ i, j | i = 1, j = 1 } : 0 ;
{ i, j | i >= 2, j = 1 } : v2[i-1,m] ;
{ i, j | j >= 2 } : scansum(a,v1[i,1]) ;
esac ;
v2[i,j] = case
{ i, j | j = 1 } : v1[i, m] ;
{ i, j | j >= 2 } : scansum(b,v2[i,1]) ;
esac ;
Comme la détection s'est faite à i fixé, l'opérateur
scansum n'est pas une procédure (ou un système dans
la terminologie Alpha). En effet, cet opérateur
nécessite des entrées et produit des sorties
à chaque i fixé. De plus, les sorties produites à
i peuvent être nécessaires pour calculer les entrées
requises à i'>i. L'opérateur scansum doit être
vu comme une macro-définition dont les arguments sont purement
textuels.
La normalisation partielle repose sur la notion de profondeur d'une
dépendance (i.e. d'une référence d'une équation à une autre).
Il a été vu qu'à chaque dépendance était associée une
inégalité avec l'ordre <. Cet ordre peut être vu comme la
disjonction de plusieurs prédicats linéaires, les <i :
|
|
|
| " iÎ{0,...,Ne,e'-1}, |
| (e,z)<i(e',z') Û z[1... i] = z'[1... i] Ù z[i+1]<z'[i+1], |
|
|
|
|
|
| (e,z)< |
|
(e',z') Û z[1... Ne,e'] = z'[1... Ne,e']
Ù e< e' |
|
|
|
" zÎ Dd, z[1... p']=L(z)[1... p']
(le domaine de la dépendance est Dd et sa transformation
affine L).
Considérons le petit programme ci-dessous :
DO i=1,n
a(i)=f(i) (v1)
END DO
DO i=1,n
b(i)=a(i)+c(i) (v2)
END DO
La transformation de la dépendance sur a entre v1 et
v2 est l'identité : L(i)=i donc la quasi-profondeur est 1.
Cependant, comme aucune boucle commune n'englobe v1 et v2 alors
Nv1,v2=0 et donc la profondeur de la
dépendance est 0.
En fait, il suffit de ne prendre en compte que les dépendances
dont la quasi-profondeur est supérieure ou égale à p.
Ces dépendances comprennent forcément les dépendances de profondeur
supérieure ou égale à p d'après (7.7). Donc, toutes
les dépendances des boucles de profondeur au moins p seront prises en
compte (il ne serait pas valide, sinon, de chercher à détecter des
récurrences relatives à ces boucles). De plus, cet ensemble de
dépendances ne peut pas contenir de circuit dont un arc serait une
dépendance de profondeur inférieure strictement à p (un circuit
de ce type peut faire échouer la normalisation partielle pour
la profondeur p).
-
Preuve:
-
Pour montrer l'absence de tels circuits il suffit de
montrer qu'un circuit dont un des arcs est une dépendance de profondeur
strictement inférieure à p (mais de quasi-profondeur supérieure
ou égale à p) comporte forcément une dépendance de quasi-profondeur
strictement inférieure à p.
D'après (7.6), la première dépendance ne peut exister
qu'entre deux équations e et e' telles que Ne,e'<p et e < e'.
Supposons que le circuit ne possède que des dépendances de
quasi-profondeur supérieure ou égale à p. Montrons que
pour tout successeur e'' de e' dans le circuit la propriété
suivante est vraie :
P(e'') º e < e'' Ù Ne,e''<p .
La propriété P(e') est vraie. Si P(e'') est vraie,
vérifions que P(e''') est vraie avec e''' successeur direct
de e'' dans le circuit. Deux cas se présentent :
-
La dépendance entre e'' et e''' donne lieu à un prédicat
de séquencement de la forme de (7.5). Dans ce cas la
quasi-profondeur et la profondeur sont identiques, donc la profondeur
de la dépendance est supérieure ou égale à p. Il en découle
que Ne'',e'''>p. Il est impossible que e'''< e car puisque
e < e'', l'égalité (7.4) impliquerait que
Ne''',e'' soit inférieur à Ne,e''<p. Donc e < e'''.
De plus :
-
soit e''< e''', auquel cas (7.4) implique
Ne,e''<p ;
- soit e'''< e'', dans ce cas comme Ne,e''<p et
Ne''',e''>p alors (7.4) implique que
Ne,e'''=Ne,e''<p.
- La dépendance entre e'' et e''' donne lieu à un prédicat
de séquencement de la forme de (7.6). Ceci implique directement
e''< e''' donc par transitivité e< e'''. De plus l'inégalité
(7.4) implique que Ne,e'''£ Ne,e''<p.
Si les successeurs e'' de e' dans le circuit sont tels que e'< e'',
alors e< e'', et e ne peut pas être son successeur dans le circuit,
une contradiction.
Intuitivement, cette preuve montre que par des références de
quasi-profondeur supérieure ou égale à p, une opération
dans une boucle de profondeur p
ne peut pas désigner des valeurs calculées dans une itération
précédente de cette boucle.
Donc, en résumé, deux schémas sont envisageables. Une
normalisation globale qui prend en compte toutes les dépendances
du système. Cette normalisation est rapide mais peu efficace ; des
récurrences peuvent ne pas être détectées.
La normalisation partielle, consiste à ne prendre en compte que les
dépendances de quasi-profondeur supérieure ou égale à un p
donné. La première normalisation se fait avec p le plus grand possible.
Les récurrences pour cette profondeur p sont détectées. Puis le
processus est itéré jusqu'à p=0.
| 8.2.3 |
Raffinement des références |
|
Ces deux schémas peuvent encore être améliorés. Si les dépendances
sont calculées au niveau des clauses plutôt qu'au niveau des équations,
il est possible de construire un graphe plus précis pour le système : le
graphe des clauses. Les sommets de ce graphe sont les clauses et les arcs
les dépendances entre les clauses.
Il est facile de calculer le graphe des clauses à partir du système
d'équations. Soit une clause c de domaine de définition Dc.
Supposons que cette clause fasse référence à une équation e
avec une transformation affine L (cette information se lit
directement dans le système d'équations), alors c fait référence
à une clause c' de l'équation e avec la transformation L ssi :
L-1( Dc')Ç Dc ¹ Ø
.
Le domaine Dc' est le domaine de définition de c' et
l'ensemble L-1( Dc') représente la pré-image de
l'ensemble Dc' par la transformation L, c'est-à-dire
l'ensemble des points z tels que L(z) est un point de
Dc'.
La normalisation sera plus efficace dans le graphe des clauses puisque
certains circuits artificiels qui apparaissent dans le graphe des
équations n'apparaissent pas dans le graphe des clauses.
Considérons la boucle Fortran ci-dessous :
DO i=1,2*n
x(i)=x(2*n-i+1) (v)
END DO
Le système correspondant est :
x : { i | 1 <= i <= 2*n } of real ;
v : { i | 1 <= i <= 2*n } of real ;
v[i] = case
{ i | 1 <= i <= n } : x[2*n-i+1] ;
{ i | n+1 <= i <= 2*n } : v[2*n-i+1] ;
esac ;
Les clauses sont nommées par le nom de leur équation et par
le numéro d'ordre de la clause dans l'équation. Par exemple
la première clause de v est v.0.
La seule clause référençante est v.1, la transformation
associée est L : i|® 2n-i+1. Il faut vérifier si
v.1 référence v.0. Calculons L-1(Nn*) :
le résultat est {n+1,...,2n}. Donc v.1 référence bien
v.0. Il faut aussi vérifier si v.1 se référence elle-même.
Comme l'ensemble L-1({n+1,...,2n}) est Nn*,
son intersection avec le domaine de définition de v.1 est vide ;
la réponse est donc négative.
Le graphe des équations comporte une boucle, ce qui peut inhiber
la normalisation dans le cas où v est incluse dans un
sous-système fortement connexe. Par contre le graphe des
clauses ne comporte pas de circuit :
Le calcul du graphe des clauses est coûteux car il nécessite
plusieurs calculs de pré-image de convexes et d'intersections
de convexes pour chaque référence à une équation.
De plus, comme les références aux clauses sont plus nombreuses
que les références aux équations, l'étape de normalisation
prendra plus de temps. C'est le prix à payer pour une plus grande
efficacité de la normalisation.
| 8.3 |
Formalisation de la substitution |
|
La normalisation du système d'équations repose sur la substitution
d'équations ou de clauses.
Intuitivement la substitution
dans un système d'équations consiste à remplacer la référence
à une équation par l'expression de cette équation. Vue la forme
particulière de nos équations il ne s'agit pas seulement d'un
remplacement textuel. En effet il n'existe pas une seule expression
pour une équation mais autant d'expressions que l'équation possède
de clauses. Remplacer la référence à une équation dans une clause
va donc conduire à éclater la clause en plusieurs autres clauses,
ce qui implique des opérations sur les convexes telles que l'intersection
et le calcul de pré-image. Ce n'est qu'après l'éclatement que le
remplacement textuel peut être effectué.
Dans le système suivant
v1 : { i | 1 <= i <= 2*n } of real ;
v2 : { i | 1 <= i <= 2*n } of real ;
v1[i] = case
{ i | 1 <= i <= n } : x[2*n-i+1] ;
{ i | n+1 <= i <= 2*n } : v2[2*n-i+1] ;
esac ;
v2[i] = case
{ i | i = 1 } : v1[i] ;
{ i | i >= 2 } : v2[i-1] + v1[i] ;
esac ;
La référence à v1 dans la seconde
clause de v2 peut être remplacée par l'expression de v1.
Mais comme cette expression est différente suivant les valeurs de
i, il faut d'abord éclater v2.1 en deux clauses. Le
domaine de la première sous-clause est { i | 2<=i<=n } et celui
de la seconde { i | n+1<=i<=2*n }. Cela conduit à un nouveau
système :
v1 : { i | 1 <= i <= 2*n } of real ;
v2 : { i | 1 <= i <= 2*n } of real ;
v1[i] = case
{ i | 1 <= i <= n } : x[2*n-i+1] ;
{ i | n+1 <= i <= 2*n } : v2[2*n-i+1] ;
esac ;
v2[i] = case
{ i | i = 1 } : v1[i] ;
{ i | 2 <= i <= n } : v2[i-1] + x[2*n-i+1] ;
{ i | n+1 <= i <= 2*n } : v2[i-1] + v2[2*n-i+1] ;
esac ;
Nous allons voir dans cette section comment formaliser le calcul des
domaines de définition des sous-clauses.
| 8.3.1 |
Substitution d'équation |
|
Une substitution d'équation consiste à remplacer dans toutes les
clauses d'une équation la référence à une autre équation
par l'expression de cette équation. Comme l'équation source
(celle qui est référencée) peut contenir plusieurs clauses,
chaque clause de l'équation cible (celle qui référence)
peut éclater en plusieurs autres clauses.
Plus formellement, considérons deux équations e et e' :
|
zÎ De, ve(z)= |
ì
ï
í
ï
î |
| Expe1(z) |
if zÎ De1 |
·
·
· |
| Expem(z) |
if zÎ Dem |
|
|
,
zÎ De', ve'(z)= |
ì
ï
í
ï
î |
| Expe'1(z) |
if zÎ De'1 |
·
·
· |
| Expe'k(z) |
if zÎ De'k |
|
.
|
Expel(ve'(L(z))) ,
où L est une transformation affine.
La substitution de la référence à e' dans la clause numéro l
de e produit les nouvelles clauses suivantes :
|
|
| Expel(Expe'1(L(z))) |
if zÎ Del Ç L-1( De'1) |
·
·
· |
| Expel(Expe'k(L(z))) |
if zÎ Del Ç L-1( De'k) |
|
-
de substituer textuellement les Expe'i(L(z)) dans
l'expression Expel ;
- de calculer les pré-images des domaines De'i et de les
intersecter avec Del. Si les intersections sont vides
(de points entiers) la clause correspondante n'est jamais utilisée
et donc peut être supprimée.
Il peut rester des références à l'équation cible dans les nouvelles
clauses donc le procédé d'éclatement doit être à nouveau
appliqué à ces nouvelles clauses et ainsi de suite.
Si nl représente le nombre de références
à l'équation source dans la clause numéro i de l'équation cible
alors le nombre d'opérations sur les convexes nécessaires pour
la substitution est de l'ordre de
ål=1m knl
.
L'exponentielle dans cette complexité est quelque peu factice car, en
pratique, les nl sont le plus souvent nuls ou égaux à 1.
| 8.3.2 |
Substitution de clause |
|
Comme vu dans la section 7.2, une normalisation plus efficace
s'appuie sur des références entre clauses. Cette normalisation utilise
non plus des substitutions d'équation mais des substitutions de clause.
Une substitution de clause consiste à remplacer, dans une clause,
une référence à une autre clause par l'expression de cette dernière.
Soient deux clauses c de l'équation e et c' de l'équation e'
telles que c référence e' :
|
|
| c |
º |
Expc(ve'(L(z))) |
if |
zÎ Dc |
| c' |
º |
Expc'(z) |
if |
zÎ Dc' |
|
|
|
| Expc(Expc'(L(z))) |
if |
zÎ Dc Ç L-1( Dc') |
| Expc(ve'(L(z))) |
if |
zÎ Dc - L-1( Dc') |
|
| 8.3.3 |
Conservation de l'ordre |
|
Les substitutions d'équation et de clause conservent l'ordre d'un
système, c'est-à-dire qu'après une substitution une inégalité du
type de (7.3) est toujours associée à chaque référence.
-
Preuve:
-
En effet les seules références ajoutées dans le système
sont celles apportées par les expressions des clauses sources.
Appelons r la référence à substituer, e et c la clause
et l'équation dans laquelle elle se trouve, e' l'équation
cible et c' une des clauses de e' (une seule s'il s'agit d'une
substitution de clause) et L la transformation affine
associée à r. Pour cette référence l'inégalité
(7.3) s'écrit :
|
" zÎ Dr, (e,z) < (e',L(z)) . |
|
" zÎ Dr', (e',z) < (e'',L'(z)) . |
" zÎ Dr''= DrÇ L( Dr'),
(e,z) < (e'',L'°L(z))
C'est à dire l'égalité (7.3) pour r''.
La preuve précédente repose sur la transitivité de l'ordre
strict <. En fait cette transitivité n'a jamais été
démontrée formellement jusqu'à présent. La propriété
(7.4) donne une opportunité de démonstration.
Soient trois opérations (e1,z1), (e2,z2) et (e3,z3).
Supposons que
(e1,z1)< (e2,z2) Ù (e2,z2)< (e3,z3)
.
Ceci implique les systèmes suivants :
|
z1[1... Ne1,e2] « z2[1... Ne1,e2] Ú |
|
z1[1... Ne1,e2] = z2[1... Ne1,e2] Ù e1 < e2 |
|
z2[1... Ne2,e3] « z3[1... Ne2,e3] Ú |
|
z2[1... Ne2,e3] = z3[1... Ne2,e3] Ù e2 < e3 |
-
Premier cas Ne1,e2<Ne2,e3,
-
soit (7.10) est vraie et par (7.4) :
|
z1[1... N |
|
] « z2[1... N |
|
] Ù
z2[1... N |
|
] |
|
z3[1... N |
|
]
,
|
z1[1... Ne1,e3]« z3[1... Ne1,e3] .
- soit (7.11) est vraie alors par (7.4) :
|
z1[1... N |
|
] = z2[1... N |
|
] Ù e1 < e2
.
|
z1[1... Ne1,e3]« z3[1... Ne1,e3] ,
soit
z1[1... Ne1,e3] = z3[1... Ne1,e3] Ù e1 < e3
.
- Second cas Ne1,e2>Ne2,e3,
-
soit (7.12) est vraie et par (7.4) :
|
z2[1... N |
|
] « z3[1... N |
|
] Ù
z1[1... N |
|
] |
|
z2[1... N |
|
]
,
|
z1[1... Ne1,e3]« z3[1... Ne1,e3] .
- soit (7.13) est vraie alors par (7.4) :
|
z2[1... N |
|
] = z3[1... N |
|
] Ù e2 < e3
.
|
z1[1... Ne1,e3]« z3[1... Ne1,e3] ,
soit
z1[1... Ne1,e3] = z3[1... Ne1,e3] Ù e1 < e3
.
- Troisième cas Ne1,e2=Ne2,e3.
Si (7.10) est vraie ou si
(7.12) est vraie alors
z1[1... Ne1,e3]« z3[1... Ne1,e3]
.
Sinon
z1[1... Ne1,e3] = z3[1... Ne1,e3] Ù e1 < e2 < e3
.



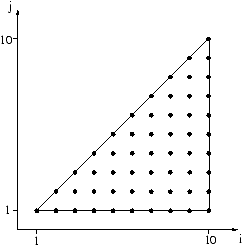



 { i,j | 1 <= i <= 10, 1 <= j <= i }
{ i,j | 1 <= i <= 10, 1 <= j <= i }