Génération de code

Chapter 14

Génération de code

À ce niveau de l'étude les réductions et les scans sont extraits du programme source et une base de temps a été calculée. La dernière étape est la génération de code du programme parallèle. Ce chapitre donne les premières briques d'une génération automatique de code. Tout d'abord il est parfois nécessaire d'aligner les vecteurs directeurs des opérateurs Scan sur les dimensions des tableaux pour pouvoir utiliser les primitives de calculs de scans de la machine cible. La section 12.1.1 indique sous quelles conditions ce changement de base peut s'effectuer. Il est ensuite montré que deux squelettes différents de code parallèle peuvent être générés pour un scan donné. Il est difficile de dire lequel des deux codes est le plus efficace. Nous présentons tout de même une heuristique de choix du code en fonction du type de scan et de la machine cible pour laquelle le code doit être généré. Les différences entre les deux codes sont explicitées sur un exemple.

14.1

Génération de code pour réductions et scans

Calculer une base de temps permet de trouver un bon programme parallèle pour une machine idéale (nombre infini de processeurs, UAL avec un nombre infini d'entrées). Cependant, sur une machine réelle, le programme parallèle brut peut avoir des performances décevantes. La phase de génération de code doit donc être optimisée pour tenir compte des particularités d'une machine réelle.

14.1.1

Alignement des directions d'un scan

Pour pouvoir utiliser les primitives de réduction ou de scan implantées sur les machines actuelles, les directions de l'opérateur Scan doivent nécessairement être alignées avec les dimensions des tableaux (e.g. pour une matrice, il n'est possible de sommer que des lignes ou des colonnes). En conséquence toutes les réductions ou scans détectés avec des vecteurs de directions non canoniques ne peuvent pas être exploités directement. Il est toujours possible d'effectuer un réarrangement des données à l'exécution lors de la phase de stockage des valeurs du scan. L'inconvénient de cette méthode est d'augmenter le temps d'exécution du programme. Autant effectuer directement le changement de base équivalent au niveau de l'opérateur Scan dans le texte du programme parallèle. La proposition suivante montre qu'il est possible, sous certaines conditions, de modifier les vecteurs directeurs d'un opérateur Scan sans modifier les valeurs calculées par cet opérateur.

Proposition 12 [Changement de base de l'opérateur Scan]
Si T est une transformation affine bijective et T_l la transformation linéaire associée, il vient :

T(Scan( D

,(e_i)

iÎN_k^*

,b,d,g))

Scan(T( D

),(T_l(e_i))

iÎN_k^*

,b,d° T^-1, g° T^-1) .

Preuve:

Notons u le tableau multi-dimensionnel calculé par le premier Scan et v celui calculé par le second. D'après la définition du Scan, v est défini par :

" zÎ T( D), v(z)=

ì
ï
ï
ï
ï
ï
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
ï
ï
ï
ï
ï
î

z=min

T( D)

T_l(e₁),...,T_l(e_k)

(z)

g(T^-1(z))

sinon si

z=min

T( D)

T_l(e₂),...,T_l(e_k)

(z)

f_T(z,v(max

T( D)

T_l(e₂),...,T_l(e_k)

(z-T_l(e₁))))

...

sinon si

z=min

T( D)

T_l(e_k)

(z)

f_T(z,v(max

T( D)

T_l(e_k)

(z-T_l(e_k-1))))

sinon

f_T(z,v(z-T_l(e_k))) ,

avec f_T définie comme étant : f_T=l zx.b(x,d(T^-1(z))) .

D'après la définition du minimum dans un convexe (voir 9.2),

min

T( D)

T_l(e₁),...,T_l(e_k)

(T(z)) ,

désigne le vecteur

T(z)-

i=1

n_i.T_l(e_i) où

(n₁,...,n_k)= lexmax(µ₁,...,µ_kÎN

^k | T(z)-

i=1

µ_i.T_l(e_i)Î T( D))

Comme la transformation T est bijective, l'expression (12.1) désigne l'image par T du vecteur

min

e₁,...,e_k

(z) .

Il en est de même pour le maximum dans un convexe. Le tableau v peut donc être aussi défini par :

" zÎ D, v(T(z))=

ì
ï
ï
ï
ï
ï
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
ï
ï
ï
ï
ï
î

T(z)=T(min

e₁,...,e_k

(z))

g(z)

sinon si

T(z)=T(min

e₂,...,e_k

(z))

f(z,v(T(max

e₂,...,e_k

(z-e₁))))

...

sinon si

T(z)=T(min

e_k

(z))

f(z,v(T(max

e_k

(z-e_k-1))))

sinon

f(z,v(T(z)-T_l(e_k))) ,

avec f définie comme étant : f=l zx.b(x,d(z)) .

Il en découle que, sur D, u est identique à v° T.

Le principe du changement de base est de trouver l'application T transformant les directions du scan en vecteurs colinéaires aux vecteurs canoniques. Une méthode est de compléter la famille des directions de l'opérateur Scan pour obtenir une base (dans le cas d'un opérateur Scan multi-directionnel c'est possible si ses directions sont indépendantes). Il suffit ensuite d'inverser la matrice formée par la base de vecteurs. Un problème est que nous ne manipulons que des domaines de définition qui sont des convexes (plus exactement des polyèdres entiers, c'est-à-dire les points entiers inclus dans le polyèdre). Or le changement de base implique une transformation du domaine de définition D de la récurrence et seule une transformation uni-modulaire ¹ transforme un polyèdre entier en un autre polyèdre entier [45]. En conséquence, il n'est pas toujours possible d'appliquer un changement de base pour que les directions de l'opérateur soient alignées suivant les vecteurs canoniques. Pratiquement cela signifie que les primitives des machines parallèles ne peuvent pas toujours être utilisées ; il faut soit exécuter ces scans en séquentiel, soit écrire des procédures plus complexes (mais forcément moins optimisées) que les primitives disponibles.

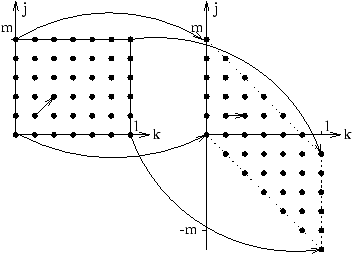
Considérons le scan ci-dessous qui calcule le tableau multi-dimensionnel u :
Scan( { 1 <= i <= n, 0 <= j <= m, 0 <= k <= l }, ( [0,1,1] ),
      +, s[i,j,k], s[i,j,k] )
La famille de vecteurs

æ
ç
ç
è

1

0

0
ö
÷
÷
ø æ
ç
ç
è

0

1

0
ö
÷
÷
ø æ
ç
ç
è

0

1

1
ö
÷
÷
ø ,
est une base pour le domaine de définition du Scan. Sa matrice inverse M_T est :

æ
ç
ç
è

1 0 0

0 1 -1

0 0 1
ö
÷
÷
ø .
Cette matrice est uni-modulaire (son déterminant est égal à 1). La fonction linéaire associée à M_T est notée T. Donc le tableau u est identique au tableau v° T où v est le tableau calculé par :
Scan( { 1 <= i <= n, 0 <= j+k <= m, 0 <= k <= l }, ( [0,0,1] ),
      +, s[i,j+k,k], s[i,j+k,k] )
La transformation du domaine de définition (pour un i fixé) et de la direction de l'opérateur Scan est illustrée sur le schéma ci-dessous.

14.1.2

Les deux types de génération de code

Nous cherchons dans la suite de cette section à générer du code efficace pour un opérateur Scan donné. La tâche est relativement complexe car un opérateur Scan peut représenter un nombre de scans dépendant des paramètres de structure. Il est donc possible d'extraire deux types de parallélisme d'un tel opérateur : le parallélisme intra-scans (en utilisant l'associativité des opérateurs) et le parallélisme inter-scans (en utilisant le fait que deux scans peuvent être calculés simultanement). L'algorithme qui vient immédiatement à l'esprit pour implanter un opérateur Scan est d'effectuer chaque scan dès que toutes ses données sont prêtes. Nous appelons le code correspondant à cet algorithme le code naïf. L'inconvénient de ce code est qu'il concentre tout le calcul dans un seul front. C'est sans effet sur une machine idéale capable de calculer un scan en une unité de temps, par contre c'est préjudiciable sur une machine n'ayant pas de primitive efficace de calcul de scan. Un autre schéma de génération de code est d'effectuer les opérations de calcul des scans au plus tôt. Ce schéma est plus particulièrement applicable aux scans de type réduction. En effet, dès qu'une donnée d'une réduction est prête il est possible de l'intégrer au résultat partiel de cette réduction. Le code correspondant à ce schéma de génération de code est appelé code asap, de l'acronyme anglais As Soon As Possible.

Considérons la réduction calculant la somme des éléments a(1) à a(n). Supposons que la base de temps pour le tableau a (i.e. la date à laquelle ses différents éléments sont prêts) soit q_a(i)=n-i. La génération de code naïve va produire le programme suivant :
      DO t=0,n-1
C       Calcul des éléments de a
        IF (t.EQ.n-1) THEN
          s=sum(a,1,n)
        END IF
      END DO
Sur la machine idéale la valeur de s est prête au temps n, mais sur une machine réelle, le calcul de la somme prendra un temps approximativement inversement proportionnel au nombre de processeurs qu'elle possède. La somme ne sera donc disponible que vers le temps n+n/p. Or il est possible d'écrire un code optimal même pour une machine mono-processeur :
      DO t=0,n-1
C       Calcul des éléments de a
        s=s+a(n-t)
      END DO
La valeur de s est alors disponible au temps n. Dans ce code les données sont accumulées sur s dès qu'elle sont prêtes, il s'agit du code asap.

Nous verrons, dans la section 12.1.4, qu'il est n'est pas facile de déterminer dans le cas général lequel du code naïf ou asap est le plus efficace.

14.1.3

Génération de code naïve

Pour formaliser la génération de code naïve, considérons un scan quelconque :

Scan( D

,(e_i)

iÎ{1,...,k}

,b,d,g)° f ,

où f représente la transformation d'extraction des résultats du scan. Si la transformation f n'est pas surjective, le scan est qualifié de scan dégénéré. Dans ce cas, les valeurs calculées par le scan ne sont pas toutes utilisées, c'est le cas des réductions. Notons q la base de temps du scan (calculé comme décrit dans la section 11.3). Notons q_d la base de temps des valeurs du scan (i.e. de la lambda-expression d). Soient t1 et t2, respectivement le minimum et le maximum de q_d sur son domaine de définition. Le scan fait partie de l'expression d'une clause, nous noterons c cette clause et D_c son domaine de définition. Les seules valeurs du scan nécessaires à la clause c sont les valeurs du domaine D'=f( D_c). Ce domaine est réduit à un point par récurrence si l'opérateur Scan représente des réductions. Avec ces notations il est possible d'exprimer le code parallèle naïf associé au scan.

DO t=t1,t2 C Calcul des vecteurs d'itération des résultats partiels de scansC à effectuer au temps t. Seul le dernier résultat de chaque scanC est pris en compte (calcul du max). Soit I l'ensemble{z | q(z)=t}Çmax_e_₁_,...,e_{_k}^D^'( D')C Exécution, en parallèle, des scans dont le dernier résultat partielC est prêt. Vu la manière dont est calculé l'ordonnancement il estC certain que toutes les données de ces scans sont prêtes. DO ALL zÎI C L'ensemble P(z) regroupe les vecteurs d'itérations des donnéesC du scan dont le vecteur du dernier résultat est z. Appliquer le scan surP(z)² END DO END DO

Dans ce code les scans ne sont déclenchés que lorsque toutes leurs données sont prêtes. Plus exactement un scan est lancé lorsque le calcul de son dernier résultat partiel utilisé peut être effectué. Le scan est effectué avec toutes ses données. Cela signifie que, si le dernier résultat partiel utilisé n'est pas le dernier résultat partiel du scan, des opérations inutiles sont effectuées. Ces opérations inutiles correspondent à des opérations inutiles dans le programme séquentiel source.

14.1.4

Génération de code asap

Nous reprenons dans cette sous-section les notations déjà définies pour exprimer le code naïf (cf section 12.1.3). De façon formelle, le principe du code asap est d'accumuler, dans un premier temps, toutes les valeurs précédant (au sens du parcours du scan) un point z de D' dans une variable temporaire associé à z. Dans un second temps une primitive de calcul de scan est appliquée sur les variables temporaires associées aux points de D'. Pour tout point z de D définissons S(z) le point tel que :

(z)=z+

i=1

l_i.e_i où

(l₁,...,l_k)= lexmin(µ₁,...,µ_kÎN

^k | z+

i=1

µ_i.e_iÎ f( D))

Définissons la relation d'équivalence associée :

" z,z'Î D× D

, zº

z' Û S(z)= S(z') .

La génération de code asap produit, pour un scan donné, le programme suivant :

DO t=t1,t2 C L'ensemble I regroupe les vecteurs d'itération des données des scansC calculées au cycle précédent. Soit I l'ensemble{z | q_d(z)=t-1}C L'ensemble I est quotienté : les vecteurs d'itération des données àC accumuler sur le même temporaire se retrouve dans la même classeC d'équivalence. Quotienter I parº_S Soit C l'ensemble des classes d'équivalence de I C Les différentes données peuvent être accumulées en parallèle dansC leurs variables temporaires respectives. DO ALL EÎC C Calcul du vecteur d'itération s associée à la variable temporaireC qui sert d'accumulateur pour une classe d'équivalence. Soit s l'image par Sd'un élément de E C Accumulation des données d'une classe d'équivalence sur saC variable temporaire. temp(s)=réduction(temp(s),E) C Si les dernières valeurs d'un scan viennent d'être accumulées, ilC faut effectuer le scan partiel sur les temporaires d'accumulation. IF s=max_e_₁_,...,e_{_k}^D(s)THEN Soit F l'ensembleP(s) Appliquer le scan sur temp( S(F)) END IF END DO END DO

Le tableau temp est un tableau temporaire représentant l'espace d'accumulation des scans finaux. L'intérêt de ce code est que les opérations calculant les scans se font au plus tôt. Il n'y a pas d'amélioration sur la latence théorique : t2+1. En revanche les opérations sont mieux réparties, contrairement à la génération de code naïve qui produit un code nul pour la plupart des fronts et concentre le calcul des scans sur quelques fronts. Le gain obtenu par l'utilisation du code asap dépend complètement de la nature du scan, de la base de temps de ses données et du type des autres opérations à exécuter entre t1 et t2.

Si la récurrence est un scan non-dégénéré, les deux codes sont identiques car S est une bijection. Il n'est donc pas possible d'accumuler par anticipation. Toutes les opérations sont effectuées par le scan final. Ce cas pourrait être optimisé si des primitives de calcul incrémental de scans existaient sur la machine cible (i.e. des primitives capables d'initier un calcul de scan avec des données incomplètes puis de mettre à jour les résultats au fur et à mesure de la disponibilité des données restantes). Pour l'instant aucune machine parallèle ne dispose de telles primitives ; elles sont très difficiles à programmer de façon efficace.

Dans le cas où le scan est dégénéré, il est généralement possible de prendre de l'avance dans les opérations. Plus le scan est dégénéré et plus le nombre de variables d'accumulation est faible (pour une réduction une seule variable est nécessaire). L'intérêt d'avoir un faible nombre de variables d'accumulation est qu'il y a un plus grand nombre de données à accumuler sur chaque variable, donc un plus grand nombre d'opérations à effectuer à l'avance. Pour pouvoir prendre de l'avance sur le calcul du scan, il faut aussi que la base de temps des données soit favorable, c'est-à-dire que les dates auxquelles les données sont prêtes doivent être bien réparties entre t1 et t2 et que l'intervalle entre t1 et t2 doit être suffisamment grand. Sinon, seuls quelques fronts entre t1 et t2 comporteront des pré-calculs pour le scan.

Par exemple, si q est constante, le code généré va se résumer à une réduction au temps t1 (égal, ici, à t2) suivi d'un scan sur une valeur. En fait, il est impossible de prendre de l'avance sur les opérations du scan puisque toutes les valeurs sont prêtes en même temps. Il faut noter que même dans ce cas une optimisation est effectuée puisque le scan est remplacé par une réduction (une réduction est généralement exécutée deux fois plus rapidement que le scan correspondant).

14.2

Comparaison du code naïf et du code asap

Dans cette section nous tentons de quantifier le gain, en terme de temps d'exécution, apporté par le code asap par rapport au code naïf. L'ensemble des opérations à exécuter à la date t, hors les opérations du scan, est noté O(t). Le temps mis pour exécuter un ensemble d'opérations O sur la machine cible est noté d(O). Soit S_n(t) l'ensemble des opérations nécessaires au calcul des scans du code naïf qui s'exécutent au temps t. Avec ces notations le temps d'exécution du code naïf est :

d_n=

tÎ {t1,...,t2}

d( O(t)È S_n(t)) .

Notons S_c(t) l'ensemble des opérations nécessaires au calcul des scans du code asap qui s'exécutent au temps t. Enfin, notons R_c(t) l'ensemble des opérations nécessaires au calcul des réductions d'accumulation du front t. Avec ces notations le temps d'exécution du code asap s'écrit :

d_c=

tÎ{t1,...,t2}

d( O(t)È S_c(t)È R_c(t))

Aucune donnée n'est connue sur les ensembles d'opération O(t). Sans hypothèse supplémentaire il est impossible de comparer d_n et d_c. En particulier il faut connaître le type de la machine cible et du langage utilisé pour construire le code parallèle.

14.2.1

Le modèle MIMD

Envisageons d'abord le cas d'un modèle d'exécution MIMD, c'est-à-dire d'une machine qui peut exécuter plusieurs opérations différentes dans le même cycle. L'intérêt de ce modèle est que les temps d'exécution des réductions d'accumulation du code asap peuvent être recouverts par les temps d'exécution des opérations classiques. Plus formellement, il est possible que les durées :

d( O(t)È S_c(t)È R_c(t)) ,

soient égales aux durées d( O(t)È S_c(t)) . Il est par contre peu probable que les temps d'exécution des scans du code naïf soient recouverts par les temps d'exécution des opérations classiques. En effet, ces scans traitent généralement un grand nombre de données, donc ont un temps d'exécution élevé même sur une machine parallèle. Le code asap est efficace pour le mode de programmation MIMD si peu de réductions d'accumulation se retrouvent dans le même front et si elles traitent un faible nombre de données.

Considérons le scan calculant les sommes partielles d'un tableau a (le tableau possède 2*n éléments) :
Scan( { -1 <= i <= 2*n-1 }, ( [1] ), +, a[i], 0 )
Supposons qu'un élément a(i) du tableau soit prêt à la date q(i)=ë i/2 û et que la fonction d'accès au scan soit f(i)=2i+1. Supposons enfin que la clause accédant au scan soit définie sur {0,...,n-1}. À chaque instant t deux valeurs sont prêtes, a(2*t) et a(2*t+1). Elles doivent être accumulées dans temp(2*t+1). Au temps t il est possible d'avancer l'exécution des deux opérations suivantes :
temp(2*t+1)=a(2*t)
temp(2*t+1)=temp(2*t+1)+a(2*t+1)
Il est probable que la plupart des O(t) ne comportent pas un nombre d'opérations multiple du nombre de processeurs. Dans le front t, la dernière vague d'opérations n'est pas complète et les deux accumulations peuvent y prendre place sans modifier le temps d'exécution du front. En définitive le scan à exécuter dans le front n traitera deux fois moins de données que le scan complet. Dans cet exemple le code asap s'exécute environ deux fois plus rapidement que le code naïf.

Il est à noter que le code asap est plus efficace si les scans représentés par l'opérateur Scan sont très dégénérés. Le cas idéal est la réduction, car plus aucun scan final n'est nécessaire. Si le code asap génère trop d'opérations d'accumulation par front, leurs temps d'exécution n'est plus recouvert par les temps d'exécution des opérations classiques. Les performances du code classique se rapprochent de celles obtenues avec un modèle d'exécution SIMD.

14.2.2

Le modèle SIMD

Comparons maintenant les temps d'exécution des codes naïf et asap dans le cadre d'un modèle de programmation data-parallèle (SIMD). L'exécution en parallèle d'opérations différentes est interdit. Cela signifie que si O₁ et O₂ sont deux ensembles d'opérations de natures différentes alors il vient d(O₁È O₂)=d(O₁)+d(O₂). La différence des durées d'exécution des codes s'écrit alors :

d_c-d_n =

tÎ{t1,...,t2}

d(R_c(t)) +

tÎ{t1,...,t2}

d(S_c(j_k)) -

tÎ{t1,...,t2}

d(S_n(i_k))

Ceci signifie qu'il n'y a un gain de temps que si la somme des temps d'exécution des réductions d'accumulation et des scans finaux dans le code asap est inférieure au temps d'exécution des scans dans le code naïf.

Soit (n_i^j)_iÎ_N_{_m}^_*_, jÎ_N_{_a}_{_{_i}}^_* la famille des nombres de données traitées par les réductions d'accumulation. La famille est doublement indicée pour décrire le fait que certaines réductions sont sensées s'exécuter au même temps : n_i^j_¹ et n_i^j_² représentent le nombre de données que traitent deux réductions ordonnancées au même instant. De la même façon, nous définissons (nc_i^j)_iÎ_N_{_m}_{_{_c}}^_*_, jÎ_N_{_b}_{_{_i}}^_* la famille des nombres de données traitées par les scans du code asap, la somme de ces nombres est notée N_c. Enfin, soit (nn_i^j)_iÎ_N_{_m}_{_{_n}}^_*_, jÎ_N_{_g}_{_{_i}}^_* la famille des nombre de données traitées par les scans du code naïf. La somme de ces nombres est notée N_n. La somme des nombres de la famille (n_i^j)_iÎ_N_{_m}^_*_, jÎ_N_{_a}_{_{_i}}^_* vaut N_n+a-N_c où a est la somme des a_i.

Preuve:: Pour prouver cette affirmation, il faut remarquer que N_c donne le nombre de variables d'accumulation, c'est-à-dire le nombre de points entiers dans le domaine D'. De plus toutes les données des scans sont accumulées et les réductions modifiant une variable d'accumulation doivent prendre en compte la valeur de cette variable. Or, il n'existe que a-N_c réductions modifiant les variables d'accumulation, les autres initialisent ces variables.

De plus la somme b des b_i est égale à la somme g des g_i.

Preuve:: Évident car il y a autant de scans dans le code asap que dans le code naïf.

Notons d_r((n_j)_jÎ_N_{_s}^_*) le temps nécessaire à la machine cible pour calculer s réductions en parallèle (sachant que la réduction j traite n_j données). Un opérateur similaire, d_s, est défini pour les scans. Avec ces notations il est possible de préciser la valeur de la différence des durées d'exécution :

d_c-d_n=

i=1

d_r((n_i^j)

jÎ N

a_i

) +

m_c

i=1

d_s((nc_i^j)

jÎ N

b_i

) -

m_n

i=1

d_s((nn_i^j)

jÎ N

g_i

) .

Affinons cette différence pour différents types de machines.

Cas d'une machine séquentielle

: Les temps de calcul des réductions et des scans sont

d_r((n_j)

jÎ N_r^*

)= d_r((n_j)

jÎ N_s^*

j=1

(n_j-1) .

Donc

d_c-d_n=(N_n+a-N_c-a)+(N_c-b)-(N_n-g)=0 .

Ceci montre que les deux codes effectuent le même nombre d'opérations.

Cas d'une machine parallèle sans primitive de calcul de scans

: Pour ce genre de machine l'intérêt du code asap est que plusieurs réductions pourront être exécutées dans le même temps. Pour exprimer les fonctions d_r et d_s il faut introduire la famille de booléens B_k,l associée à une famille de nombres de données (n_j)_jÎ_N_{_s}^_* (nous supposons, de plus, que n₁ est le maximum de la famille). Cette famille est définie par :

" kÎN

n₁

, " lÎN_s^*, B_k,l=(n_l>k)

Si la machine possède p processeurs les durées s'expriment comme suit :

d_r((n_j)

jÎ N_r^*

)= d_r((n_j)

jÎ N_s^*

n₁

k=1

é
ê
ê
ê

l=1

B_k,l

ù
ú
ú
ú

L'addition des booléens s'entend comme l'addition d'entiers, soit 0 soit 1. Si B est la famille booléenne associée à (n_i^j), B' celle associée à (nc_i^j) et B'' celle associée à (nn_i^j), la différence de temps d'exécution entre les deux codes devient :

d_c-d_n=

i=1

n₁ⁱ

k=1

é
ê
ê
ê

a_i

l=1

B_k,lⁱ

ù
ú
ú
ú

m_c

i=1

nc₁ⁱ

k=1

é
ê
ê
ê

b_i

l=1

B'_k,lⁱ

ù
ú
ú
ú

m_n

i=1

nn₁ⁱ

k=1

é
ê
ê
ê

g_i

l=1

B''_k,lⁱ

ù
ú
ú
ú

Ce qui conduit à l'encadrement ci-dessous :

m_n

i=1

nn₁ⁱ £ d_c-d_n <

i=1

n₁ⁱ +

m_c

i=1

nc₁ⁱ .

Preuve:

En effet, puisque é xù est compris entre x et x+1, la différence des durées est encadrée par :

i=1

n₁ⁱ

k=1

a_i

l=1

_k,lⁱ+

m_c

i=1

nc₁ⁱ

k=1

b_i

l=1

'_k,lⁱ+

m_n

i=1

nn₁ⁱ

k=1

g_i

l=1

B''_k,lⁱ

m_n

i=1

nn₁ⁱ ,

i=1

n₁ⁱ

k=1

a_i

l=1

_k,lⁱ+

m_c

i=1

nc₁ⁱ

k=1

b_i

l=1

'_k,lⁱ+

m_n

i=1

nn₁ⁱ

k=1

g_i

l=1

B''_k,lⁱ

i=1

n₁ⁱ +

m_c

i=1

nc₁ⁱ .

Or, d'après la définition des familles booléennes :

i=1

n₁ⁱ

k=1

a_i

l=1

_k,lⁱ+

m_c

i=1

nc₁ⁱ

k=1

b_i

l=1

'_k,lⁱ+

m_n

i=1

nn₁ⁱ

k=1

g_i

l=1

B''_k,lⁱ

(N_n+a-N_c-a)+(N_c-b)+(N_n-g)=0 .

La génération du code asap est intéressante lorsque la différence des durées est proche de la borne inférieure (il s'agit d'une valeur négative). C'est le cas lorsque les deux premiers termes de l'expression (12.2) sont peu perturbés par l'arrondi par valeur supérieure (i.e. quand la valeur du terme écrit avec l'arrondi est peu différente de la valeur du terme écrit sans l'arrondi) et lorsqu'au contraire cet arrondi augmente sensiblement le poids du dernier terme. Les conditions pour que l'arrondi ne perturbe pas un terme dépendent de trop de paramètres. Par contre, il existe une condition simple à exprimer et suffisante pour qu'un terme soit fortement perturbé par l'arrondi. Prenons, par exemple, le troisième terme de (12.2) ; il suffit que les g_i soient négligeable devant p. Dans ce cas la différence entre le terme écrit avec et sans l'arrondi est très proche de å_i=1^m_ⁿnn₁ⁱ . Sous cette hypothèse la différence des deux durées est majorée par

m_n

i=1

nn₁ⁱ+

i=1

n₁ⁱ+

m_c

i=1

nc₁ⁱ .

La différence est négative si la valeur absolue du premier terme est grande devant les valeurs des deux derniers termes. Les g_i étant petits le premier terme est de l'ordre de -N_n. Les deux autres termes sont d'autant plus petits que les a_i et les b_i sont grands et que les (n_i^j) et les (nc_i^j) pour i fixé sont équilibrés.

Dans le cas où :

les g_i sont égaux à 1 ;
les (n_i^j) pour i fixé sont identiques (idem pour les (nc_i^j)) ;
les a_i sont tous égaux à a/m et les b_i sont tous égaux à b/m_c,
la différence est alors majorée par :

-

p-1

p
N_n+

m

a
(N_n-N_c)+

m_c

b
N_c .
Si le nombre de réductions d'accumulation est grand par rapport au nombre de fronts dans lesquelles elles s'exécutent il est intéressant de générer un code asap.

En résumé, la génération du code asap est rentable si :

les scans du code naïf ne peuvent pas être exécutés en parallèle ;
les réductions d'accumulation du code asap sont nombreuses, peuvent être exécutés en parallèle et traitent approximativement le même nombre de données ;
les scans du code asap peuvent aussi être exécutés en parallèle ou sont inexistants comme dans le cas où l'opérateur Scan désigne en fait une réduction.

Cas d'une machine parallèle avec primitive de calcul de scans

: Nous étudions le cas où uniquement le parallélisme relatif au calcul des réductions et des scans est exploité. Le parallélisme entre les scans n'est pas utilisé. Les scans sont supposés implantés avec la technique du partitionnement décrite dans la section 11.2. Pour une famille de nombres de données (n_j)_jÎ_N_{_s}^_* les fonctions de durée s'écrivent :

d_s((n_j)

jÎN_s^*

)=2

æ
ç
ç
è

i=1

é
ê
ê
ê

n_j-1

ù
ú
ú
ú

ö
÷
÷
ø

d_r((n_j)

jÎN_s^*

i=1

é
ê
ê
ê

n_j-1

ù
ú
ú
ú

+p .

La différence des durées est donc :

d_c-d_n

i=1

æ
ç
ç
è

a_i

j=1

é
ê
ê
ê

n_jⁱ-1

ù
ú
ú
ú

ö
÷
÷
ø

m_c

i=1

æ
ç
ç
è

b_i

j=1

é
ê
ê
ê

nc_jⁱ-1

ù
ú
ú
ú

ö
÷
÷
ø

m_n

i=1

æ
ç
ç
è

g_i

j=1

é
ê
ê
ê

nn_jⁱ-1

ù
ú
ú
ú

ö
÷
÷
ø

La différence est encadrée par :

N_c-N_n

-2g(p+1) £ d_c-d_n <

N_c-N_n

+(a+2b)(p+1) .

Preuve:

D'après l'expression (12.3) la différence des durées est comprise entre :

i=1

a_i

j=1

(n_jⁱ-1) +2

m_c

i=1

b_i

j=1

(nc_jⁱ-1) -2

m_n

i=1

g_i

j=1

(nn_jⁱ-1)

-2g(p+1) ,

i=1

a_i

j=1

(n_jⁱ-1) +2

m_c

i=1

b_i

j=1

(nc_jⁱ-1) -2

m_n

i=1

g_i

j=1

(nn_jⁱ-1)

+(a+2b)(p+1) .

Or l'expression au numérateur de la fraction vaut :

(N_n+a-N_c-a)+2(N_c-b)-2(N_n-g)=N_c-N_n .

D'où le résultat.

La génération du code asap est intéressante pour ce type de machine lorsque les conditions suivantes sont réunies :

La borne inférieure de l'expression (12.3) est la plus petite possible. C'est à dire que N_c est minimale (l'opérateur Scan représente une réduction et non un scan) et N_n est grand (la réduction traite un grand nombre de données).
La différence doit être proche de sa borne inférieure. Si, déjà, la récurrence est une réduction le deuxième terme de l'expression (12.3) est supprimé. Il reste à minimiser l'augmentation du premier terme du à l'arrondi à la valeur supérieure. L'unique solution consiste à minimiser a. Il faut donc que le nombre de réduction d'accumulation soit faible.

En résumé le code asap ne s'impose que si l'opérateur Scan décrit une réduction et que le nombre de réductions d'accumulation est faible. Dans ce cas un gain est à attendre car les scans du code naïf sont remplacés par quelques réductions dans le code asap et qu'une réduction s'exécute environ deux fois plus vite qu'un scan.

Le fait que le fractionnement des réductions d'accumulation pénalise le code asap peut être imputé au fait que les petites réductions (avec moins ou de l'ordre de p données) sont exécutées inefficacement. Il est facile de voir que dans ce cas mieux vaut n'utiliser que n^1/2 processeurs (n est le nombre de données de la réduction). Recommençons les calculs avec de nouvelles fonctions de durée adaptées aux petites réductions :

d_s((n_j)

jÎN_s^*

)= 2

j=1

æ
ç
ç
ç
ç
ç
ç
è

é
ê
ê
ê
ê
ê
ê
ê

n_j-1

ù
ú
ú
ú
ú
ú
ú
ú

é
ê
ê
ê
ê

n_j-1

ù
ú
ú
ú
ú

ö
÷
÷
÷
÷
÷
÷
ø

j=1

é
ê
ê
ê
ê

n_j-1

ù
ú
ú
ú
ú

d_r((n_j)

jÎN_s^*

)=2

j=1

é
ê
ê
ê
ê

n_j-1

ù
ú
ú
ú
ú

La différence des durées devient (en supposant que les réductions d'accumulation traitent moins de p² données et que les scans du code naïf traitent toujours un grand nombre de données).

d_c-d_n

i=1

a_i

j=1

é
ê
ê
ê
ê

n_jⁱ-1

ù
ú
ú
ú
ú

m_c

i=1

b_i

j=1

é
ê
ê
ê
ê

nc_jⁱ-1

ù
ú
ú
ú
ú

m_n

i=1

æ
ç
ç
è

g_i

j=1

é
ê
ê
ê

nn_jⁱ-1

ù
ú
ú
ú

ö
÷
÷
ø

Cette expression est minorée par -g (p+1).

Preuve:

L'expression (12.4) est en effet minorée par

i=1

a_i

j=1

n_jⁱ-1

m_c

i=1

b_i

j=1

nc_jⁱ-1

-2

m_n

i=1

g_i

j=1

nn_jⁱ-1

-2g (p+1) .

De plus le troisième terme de cette minoration vaut exactement

-2

N_n - g

Enfin, puisque les n_jⁱ-1 sont inférieurs à p², la racine de ces nombres est supérieure à la fraction n_jⁱ-1/p. D'où les inégalités suivantes :

i=1

a_i

j=1

n_jⁱ-1

m_c

i=1

b_i

j=1

nc_jⁱ-1

i=1

a_i

j=1

(n_jⁱ-1) +

m_c

i=1

b_i

j=1

(nc_jⁱ-1)

N_n+a-N_c-a+N_c-b

N_n-b

La somme b est égale à la somme g donc l'expression (12.4) est bien minorée par -2g (p+1).

Le code asap n'apporte pas de gain réel si les réductions d'accumulation sont nombreuses et traitent un faible nombre de données. Il est, en théorie, possible d'obtenir un gain de 2g (p+1) cycles mais ce gain dépend complètement des défauts d'arrondi du troisième terme de l'expression (12.4). Il n'y a aucun moyen de prédire l'importance de ces défauts, cela dépend du nombre de processeurs et des nombres de données traitées par les scans du code naïf.

14.3

Plans pour une génération automatique de code

Cette section discute des techniques à employer pour réaliser une génération automatique de code pour des programmes contenant des récurrences (i.e. des scans et des réductions). Deux étapes doivent être automatisées. Le choix du code à générer puis la génération du code lui-même.

14.3.1

Choix du code à générer

Dans un premier temps nous présentons une méthode pour choisir le code à générer pour un opérateur Scan donné. Nous utilisons les notations et les résultats de la section 12.1.4. Comme tous les cas de figure ne sont pas envisagés dans cette section, la solution proposée est forcément heuristique. La situation est décrite par un certain nombre de paramètres :

le type du langage parallèle (i.e. modèle de programmation MIMD ou SIMD, présence ou non de primitives de calcul de scans et de réductions) ;
la fonction de transformation f utilisée par la clause pour accéder aux résultats de l'opérateur Scan ;
l'ensemble des points de l'espace d'accumulation dont la donnée correspondante est prête au temps t-1 :
Q_d(t)= { zÎ D | q_d(z)=t-1 } .
l'ensemble des points de l'espace d'accumulation correspondant à l'exécution d'un scan au temps t dans le code naïf :

Q(t)= { zÎ D | q(z)=t } Ç max

D'

e₁,...,e_k
( D') ;

Il est à noter que le langage cible peut disposer d'une primitive de calcul de scan et de réduction pour une fonction associative donnée et en être dépourvu pour une autre fonction.

La génération du code asap dans le cas général est trop complexe. Ce code ne sera utilisé que lorsque l'opérateur Scan décrit des réductions. En conséquence, il faut commencer par déterminer le type de la récurrence. En fait, l'opérateur Scan décrit une réduction ssi

" zÎ D', max

e₁,...,e_k

(z)=z .

³ Pour simplifier la vérification, il est supposé que toutes les données de l'opérateur Scan sont utilisées (dans le cas contraire le programme source exécute des opérations inutiles). La condition devient :

" zÎ D', max

e₁,...,e_k

(z)=z .

Il est facile de calculer l'enveloppe convexe de D_c à l'aide de la bibliothèque d'opérations sur les convexe de l'Irisa. Comme c'est l'enveloppe convexe qui est calculée, et non pas l'ensemble lui même, le test est approximatif. Il est cependant conservatif dans la mesure où il ne détectera pas de réduction à tort. Notons D'' l'enveloppe convexe, si la solution du problème

lexmax

ì
í
î

l | l

0 Ù z+

i=1

l_k e_kÎ D

ü
ý
þ

dans le contexte où zÎ D'' est 0, alors l'opérateur Scan décrit un ensemble de réductions. Le calcul du maximum lexicographique peut être résolu par PIP. Si ce test échoue un code naïf est généré. Sinon la prise de décision est différente suivant le type du langage parallèle.

Prenons d'abord le cas d'un modèle de programmation MIMD. D'après la section 12.1.4, il faut générer du code asap si, quelque soit le front F(t), le nombre de points contenus dans Q_d(t) est petit (par rapport au nombre de processeurs disponibles). Plusieurs méthodes peuvent être employées pour estimer le nombre de points.

Une méthode rapide mais très approximative consiste à calculer la dimension du convexe. Il suffit de prendre le nombre de variables servant à exprimer le polyèdre et d'y retrancher le nombre d'équations du système le définissant. Le nombre d'équations est facilement obtenu, par exemple, en simplifiant les inéquations du système par l'algorithme de Chernikova.
Il existe des méthodes exactes de calcul du nombre de points entiers dans un polyèdre. Les premiers travaux ont été menés par Nadia Tawbi dans le cadre du projet PAF [59, 60]. Une amélioration de cette technique se trouve dans [49]. Le problème est que le nombre de points entiers peut être une formule complexe en fonction des paramètres de structure du programme. Pour simplifier la vérification il faut extraire le terme de plus haut degré. Si ce terme dépend effectivement des paramètres de structure il est considéré que le polyèdre contient un grand nombre de points. En fait, comme les paramètres de structure peuvent être arbitrairement grands, le polyèdre peut contenir un nombre de points arbitrairement grand. Un nombre de points sera considéré petit si son terme de plus haut degré est une constante. Il est possible de raffiner le test en vérifiant que la constante est faible devant le nombre de processeurs.
Une autre technique pour vérifier qu'un polyèdre ne contient que peu de points est de calculer une intersection de convexes. Il faut commencer par trouver le point z₀ lexicographiquement minimum dans le convexe (en utilisant le logiciel PIP). La seconde étape consiste à choisir une constante e petite devant le nombre de processeurs de la machine cible. L'intersection se fait entre le polyèdre et l'hyper-cube {z₀+h | " i, h_iÎN_e}. Si l'intersection est égale au polyèdre c'est qu'il est inclus dans l'hyper-cube ; il contient peu de points.

Si ce test est positif il faut générer du code asap, sinon il faut supposer que le modèle de programmation est un modèle SIMD.

Considérons le cas d'un langage de type SIMD ne disposant pas de primitive efficace de calcul de scans. D'après la section 12.1.4, Il faut générer du code asap si,

quelque soit t, l'ensemble Q(t) contient les points correspondant à seulement quelques scans ;
il faut de plus que, quelque soit t, l'ensemble Q_d(t) contienne les points correspondant aux données de nombreuses réductions d'accumulation ;
ces données doivent être équitablement distribuées sur les réductions.

L'ensemble Q(t) peut être calculé automatiquement (plus de détails sont donnés dans la section 12.3.2). Le test sur le nombre de points dans Q(t) se fait de la même façon que le test sur Q_d(t) dans le cas du modèle MIMD. Les deux dernières conditions sont trop difficiles à vérifier. Une approximation consiste à vérifier que l'ensemble

max

e₁,...,e_k

(Q_d(t)) ,

comporte un grand nombre de points. Ce n'est qu'une approximation car cela n'assure pas que les données sont équitablement réparties sur les réductions. L'ensemble (12.6) peut être calculé automatiquement (voir la section 12.3.2). Le nombre de points peut alors être estimé par une des méthodes décrites plus haut (i.e. il faut vérifier que l'ensemble ne contient pas un petit nombre de points). Si les deux tests sont positifs, du code asap doit être généré sinon il suffit de générer du code naïf.

Enfin examinons le cas d'un langage de type SIMD disposant de primitives efficaces de calcul de scans et de réductions. D'après la section 12.1.4, le code asap est à générer lorsque, quelque soit t, Q_d(t) contient de nombreux points associés aux données de seulement quelques réductions. Pour cela il suffit de vérifier que Q_d(t) contient de nombreux points et que l'ensemble (12.6) contient, lui, seulement quelques points. Si le test est positif il faut générer du code asap sinon du code naïf.

14.3.2

Génération automatique de code

La génération de code naïf passe par le calcul des ensembles Q(t) et P(z). Le calcul de l'ensemble Q(t) se décompose en le calcul de l'ensemble

{ zÎ D | q(z)=t } ,

et le calcul de l'ensemble :

max

e₁,...,e_k

( D') .

Le premier ensemble est déjà sous la forme d'un ensemble d'inéquations affines car D est défini ainsi. Le second ensemble ne peut pas être calculé tel quel, nous faisons la même hypothèse que dans la section 12.3.1. C'est à dire que le maximum est calculé dans D et pas dans D'. Trouver un système d'inéquations caractérisant

max

e₁,...,e_k

( D') ,

ne nécessite pas de nouveau calcul. Il suffit de reprendre la solution générique L(z) du problème (12.5). L'ensemble s'écrit alors :

ì
í
î

i=1

L_k(z).e_k | zÎ D'

ü
ý
þ

En conclusion, l'ensemble (en réalité un sur-ensemble de) Q(t) est caractérisable par un ensemble d'inéquations linéaires. Plus exactement, dans le cas général L(z) est un arbre de sélection, l'ensemble Q(t) est donc une union de polyèdres décrits par des systèmes d'inéquations. À partir de ces inéquations, il est possible de déterminer un nid de boucles pour énumérer les points entiers des polyèdres. Plusieurs méthodes ont été développées pour générer ces nids de boucles, la première est basée sur l'algorithme de Fourier-Motzkin [5], une seconde sur le logiciel PIP [19], une autre utilise la bibliothèque sur les convexes de l'Irisa [62] et enfin la dernière en date [20] peut même être utilisée si l'ensemble décrit est un polyèdre à trous (i.e. n'inclut pas tous les points entiers d'un polyèdre mais par exemple un sur deux).

Les corps des nids de boucles exécutent les scans. Pour un vecteur d'itération z donné, un scan sur les données des coordonnées contenues dans P(z) doit être effectué. Une méthode de calcul de P(z) est décrite dans la section 11.3. Si les directions de l'opérateur Scan sont alignées sur les dimensions des tableaux ou si le changement de base présenté dans la section 12.1.1 est applicable le scan peut être implanté grâce à la plupart des primitives de calcul de scan existantes. Quand le domaine défini par P(z) n'est pas régulier (rectangulaire ou parallélipédique), les éléments non utilisés du tableau doivent être remplis avec l'élément neutre de l'opération. Si les directions ne peuvent pas être alignées sur les dimensions du tableau ou si la machine ne possède pas de primitives de scan, il faut utiliser une procédure respectant exactement la sémantique de l'opérateur Scan. Cette procédure est moins optimisée que ne le seraient des primitives natives.

Passons à la génération de code asap. Le squelette du code asap pour un opérateur Scan décrivant des réductions est :

DO t=t1,t2 Soit I l'ensembleQ_d(t) Quotienter I parº_S Soit C l'ensemble des classes d'équivalence de I DO ALL EÎC Soit s l'image par Sd'un élément de E temp(s)=réduction(temp(s),E) END DO END DO

L'ensemble Q_d(t) est facilement caractérisable par un ensemble d'inéquations. La fonction S dans le cas d'une réduction (avec les habituelles approximations sur D') n'est rien d'autre que max_e_₁_,...,e_{_k}^D. Le point S(z) est donc la solution générique l(z) du problème (12.5). Au lieu de calculer le quotient de Q_d(t) par º_S, il est plus simple de calculer l'ensemble (12.6). Il est possible de calculer automatiquement (12.6) en utilisant PIP de même manière que pour résoudre (12.5). Le contexte seul diffère, il devient zÎ Q_d(t). Le résultat s'écrit comme une union paramétrée par t d'ensembles définis par des systèmes d'inéquations affines. Il est donc possible d'énumérer les points entiers de l'intersection grâce à des nids de boucles. Il reste à trouver pour un de ces points i la classe d'équivalence E correspondante. Il s'agit de l'ensemble :

Q_d(t)Ç {zÎ D | S(z)=i} .

Encore une fois, cet ensemble est une union de polyèdres définis par des systèmes d'inéquations affines. Il se pose le même problème que pour le code naïf : si l'ensemble n'est pas régulier les primitives de calcul de scans classiques ne peuvent pas être utilisées.

14.3.3

Illustration sur un exemple

Le but de cette section est de montrer que le détecteur de scans couplé à un générateur de code permet une parallélisation ``sémantique'' de certains programmes. L'exemple que nous avons choisi est l'algorithme de résolution d'un système linéaire dont la matrice associé est triangulaire. Cet algorithme est la dernière phase (dite de remontée) des procédés de résolution des systèmes linéaires quelconques. L'implantation la plus courante (car la plus naturelle pour un humain) de l'algorithme de remontée est la suivante :

DO i=0,n-1 
 x(n-i)=b(i+1)                           (v1)
  DO j=1,i
    x(n-i)=x(n-i)-a(i+1,n-i+j)*x(n-i+j)  (v2)
  END DO
 x(n-i)=x(n-i)/a(i+1,n-i)                (v3)
END DO

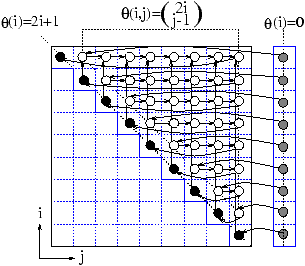
Le graphe de dépendance est dessiné ci-dessous.

Les sommets de ce graphe de dépendance représentent à la fois les opérations et les données du programme. Les sommets grisés représentent les opérations de v1 qui référencent les données b(i+1). Les sommets évidés représentent les opérations de v2 qui utilisent les données a(i+1,n-j+1). Enfin, les sommets pleins représentent les opérations de v3 qui opèrent sur les données a(i+1,n-i). La base de temps des opérations de v2 est multi-dimensionnelle. L'ordonnancement classique ne réussit pas à extraire de parallélisme du programme séquentiel. Tentons une détection de scans, le système final est :

a  : { i,j | 1<=i<=n, 1<=j<=n } of real ;
b  : { i | 1 <= i <= n } of real ;
v3 : { i | 0 <= i <= n-1 } of real ;
v3[i] = case
        { i | i = 0 } : b[1] / a[1,n] ;
        { i | i > 0 } :
          Scan( { i',j' | 1<=i'<=n-1, 0<=j'<=i }, ( [0 1] ), +,
                -a[i'+1,n-i'+j'] * v3[i'-j'], b[i'+1]
              )[i,i] / a[i+1,n-i] ;
        esac ;

Il faut maintenant calculer la base de ce système par la méthode présentée en 11. Les contraintes de causalité pour les bases de temps q(v,.) de l'opérateur Scan et q(v3,.), de l'équation v3 sont :

" iÎN_n-1^*, " jÎN_i^*, q(v,(i,i)) ³ q(v3,i-j) + 1

q(v3,0) ³ 1

" iÎN_n-1^*, q(v3,i) ³ q(v,(i,i)) +1

Ce qui peut se réécrire en :

q(v,(1,1))³ 2

" iÎ{2,...,n-1}, " jÎN_i^*, q(v,(i,i)) ³ q(v,(i-j,i-j)) + 2

q(v3,0) ³ 1

" iÎN_n-1, q(v3,i) ³ q(v,(i,i)) +1

Les bases de temps ci-dessous conviennent ;

q(v,(i,i))=2i, et q(v3,i)=2i+1

L'ordonnancement est à nouveau uni-dimensionnel. Pour décider du code à générer il faut commencer par résoudre le problème (12.5) :

lexmax

{

l | l ³ 0 Ù i Î N_n-1^* Ù j + l Î N_i

}

La solution générique est :

L(i,j)=

ì
í
î

if	1£ i £ n-1 Ù 0£ j£ i	i-j
if	i<1 Ú i> n-1 Ú j>i	^ .

Le symbole ^ indique qu'il n'y a pas de solution pour un contexte donné. Pour vérifier que les récurrences décrites par l'opérateur Scan sont bien des réductions, il faut calculer f( D_c). La fonction f est (i,j)|® (i,i) et le domaine de la clause est N_n-1^*. L'image par f est donc {(i,i) | iÎN_n-1^*}. La restriction de L(z) à ce domaine est i-i=0. Nous sommes donc en présence de réductions, le choix du type de code se fait sur le type du langage cible.

Supposons que le langage cible soit de type MIMD. Il faut estimer le nombre de points de l'ensemble Q_d(t). Cet ensemble est défini par un système d'inéquations affines :

{(i,j) | iÎN_n-1^*, jÎN_i, q(v3,i-j)=t-1}

{(i,j) | 1£ i£ n-1, 0£ j£ i, 2(i-j)=t-2} .

Dans le contexte où n est grand et t est compris entre 2 et 2n-1, le point lexicographiquement minimum z₀(t) de Q_d(t) est :

z₀(t)=

ì
ï
ï
í
ï
ï
î

t³ 4

(

-1,0)

else

(1,2-

) .

Il reste à vérifier si le convexe est inclus dans

ì
í
î

æ
ç
ç
è

+h₁-1,h₂

ö
÷
÷
ø

| 0£ h₁£ e, 0£ h₂£ e

ü
ý
þ

pour t£ 4 et dans

ì
í
î

æ
ç
ç
è

1+h₁,h₂-

ö
÷
÷
ø

| 0£ h₁£ e, 0£ h₂£ e

ü
ý
þ

pour t={2,3}. Avec e=2, les deux tests sont négatifs. Ce résultat est logique puisque le nombre d'opérations d'accumulation est de l'ordre de n. C'est trop pour pouvoir supposer que la durée d'un front n'est pas modifiée. Nous continuons l'analyse en supposant que le langage est du type SIMD mais sans primitives de calcul de scans. Vérifions que Q(t) ne comporte que peu de points. Cet ensemble s'écrit :

{ (i,j)+L(i,j).(0,1) | (i,j)Îf( D_c), q(v,(i,j))=t}

{ (i,j)+(0,L(i,j)) | (i,j)=(i',i'), 1£ i'£ n-1, 2i=t}

ì
ï
í
ï
î

t mod 2=0

{ (

) }

else

Ø .

Il comporte au plus un point. La seconde condition à vérifier est que l'ensemble ci-dessous comporte un grand nombre de points.

max

(0,1)

(Q_d(t))

{ (i,j)+L(i,j).(0,1) | (i,j)ÎQ_d(t)}

{ (i,i) | iÎN_n-1^*, jÎN_i, 2(i-j)=t-2 }

ì
ï
í
ï
î

t mod 2=0

ì
í
î

(i,i) |

-1£ i£ n-1

ü
ý
þ

else

Ø .

Pour les fronts de numéro pair l'ensemble contient un grand nombre de points. Les deux tests sont vérifiés. Un code asap doit être généré. L'ensemble (12.9) a déjà été calculé. Reste à exprimer l'ensemble

Q_d(t) Ç { (i',j')Î D | S(i',j')=(i,j) } ,

dans le contexte où (i,j) est un élément de (12.9) et t est pair.

Q_d(t) Ç { (i',j')Î D | S(i',j')=(i,j) }

{(i',j') | i'ÎN_n-1^*, j'ÎN_i', 2(i'-j')=t-2, (i',i')=(i,j)}

{(i',j') | j'=i-

+1} .

Les classes d'équivalence sont donc des singletons. L'application d'une des méthodes permettant d'énumérer les points entiers d'un convexe conduit au code ci-dessous.

v3(0)=b(1)/a(1,n)
DO i=1,n-1
  temp(i,i)=b(i+1)
END DO
DO t=2,2*n-1
  IF (MOD(t,2).EQ.0) THEN
    t2=DIV(t,2)
    DO ALL i=t2-1,n-1
      temp(i,i)=temp(i,i)-a(i+1,n-t2)*v3(t2)
    END DO
  END IF
  IF (MOD(t,2).EQ.1) THEN
    i=DIV(t,2)
    v3(i)=temp(i,i)/a(i+1,n-i)
  END IF
END DO

Ce programme parallèle est optimal. Il est à noter qu'il peut être obtenu par la méthode géométrique classique. Pour cela il faut modifier le programme Fortran initial (i.e. accumuler les produits non plus de la gauche vers la droite sur la figure mais de la droite vers la gauche) :

DO i=0,n-1
 x(n-i)=b(i+1)                          (v1)
  DO j=1,i 
   x(n-i)=x(n-i)-a(i+1,n-j+1)*x(n-j+1)  (v2)
  END DO 
 x(n-i)=x(n-i)/a(i+1,n-i)               (v3)
END DO

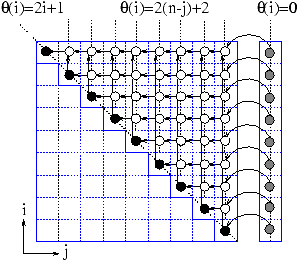
Le graphe de dépendance détaillé de ce programme est donné sur la figure ci-dessous :

En supposant que les valeurs des tableaux a et b soient calculés au temps 0, un calcul de base de temps classique va trouver un bon ordonnancement pour le programme. En effet la base de temps des opérations de l'instruction v2 (qui constituent la majeure partie des opérations du programme) est 2(n-j)+2. Ceci signifie que le programme parallèle déduit de cette base de temps peut s'exécuter en un temps de l'ordre de n²/p. D'une certaine façon la détection de scans suivie d'une génération de code asap ont parallélisé sémantiquement le programme séquentiel. C'est à dire que les opérations d'addition ont été réorganisées pour obtenir un code parallèle plus efficace.

Considérons le dernier cas : un langage cible de type SIMD avec des primitives de calcul de scans. Le test du code échoue car (12.9) contient de nombreux points. C'est donc un code naïf qui doit être généré. L'ensemble (12.8) est déjà calculé. Reste la caractérisation de l'ensemble P(i,j), avec (i,j) dans (12.8) :

P(i,j)={(i,j') | j'ÎN_i^*} .

Le code naïf se déduit de ces deux polyèdres.

v3(0)=b(1)/a(1,n)
DO t=2,2*n-1
  IF (MOD(t,2).EQ.0) THEN
    i=DIV(t,2)
    temp(0)=b(i+1)
    DO ALL j=1,i
      temp(j)=a(i+1,n-i+j)*v3(i-j)
    END DO
    v(i)=SUM_PREFIX(temp(0:i))
  END IF
  IF (MOD(t,2).EQ.1) THEN
    i=DIV(t,2)
    v3(i)=v(i,i)/a(i+1,n-i)
  END IF
END DO

La complexité de ce programme est proche de la complexité optimale si la fonction SUM_PREFIX est parallélisée. Le code asap est, cependant, encore meilleur. L'heuristique de choix du code à générer est faussée du fait que la parallélisation entre réductions d'accumulation n'a pas été envisagée dans le cas du langage SIMD possédant des primitives de calcul de scan. Heureusement, choisir à tort le code naïf n'est jamais très préjudiciable si des primitives de calcul des scans existent. Cela revient à utiliser le parallélisme intra-scans plutôt que le parallélisme inter-scans. Ce parallélisme est plus complexe à extraire donc un peu moins efficace.

1: Une tranformation uni-modulaire est telle que sa matrice associée est à coefficients entiers et possède un déterminant ègal à 1 ou -1.
2: L'ensemble P(z) est défini à la section 11.3.
3: Rappel : l'ensemble D' est l'image par f du domaine de la clause dans laquelle se trouve l'opérateur, i.e. f( D_c).