| Chapter 15 |
Étude de cas sur un processeur vectoriel |
|
Le but de cette étude de cas est de montrer qu'un code efficace
peut être obtenu en utilisant le détecteur de scans.
Un autre intérêt est de montrer quelles sont les difficultés
que pose la génération manuelle de code pour des scans.
Ces enseignements sont indispensables pour la conception d'un
système de génération automatique de code.
La machine utilisée pour les tests est un Cray Y-MP
d'entrée de gamme (horloge de 30 nano-secondes)
avec 4 processeurs. Pour calculer les scans et les réductions
en parallèle nous utilisons à la fois des primitives de la
bibliothèque du Cray et des procédures écrites pour l'occasion.
La génération du code pour les deux exemples est simplifiée
du fait que toutes les données des réductions incluses dans
les programmes sont prêtes dès l'instant 0. En conséquence
du code asap doit être généré pour les réductions et
du code naïf pour les scans.
| 15.1 |
Procédures de calcul de scans |
|
Le premier problème rencontré pour la génération de code
pour les scans et les réductions sur un Cray est l'absence de
certaines primitives de calcul de récurrences optimisées.
La bibliothèque d'algèbre linéaire du Cray (BLAS1) contient
quelques primitives de réduction optimisées pour les fonctions
somme, maximum et minimum et produit scalaire. Évidemment, la primitive
pour calculer efficacement la fonction search décrite à la
section 10.3 n'existe pas. Comme elle est utilisée dans
un de nos deux exemples, nous l'avons implanté. Cela se fait
facilement en utilisant la réduction-maximum et en utilisant
le tableau de booléens comme un tableau d'entiers contenant
uniquement des 0 et des 1. Le tableau est plus noir pour les
scans. Les seuls scans correctement optimisés que nous avons
trouvé sont ceux relatifs à l'addition et la multiplication.
Or les exemples nécessitent des scans pour la multiplication
complexe, pour le maximum et pour le minimum.
Nous avons donc été conduit à implanter nos propres scans.
La méthode utilisée est la méthode dite du partitionnement.
Par exemple, si o est la taille des registres vectoriels
de la machine, la procédure pour calculer les sommes partielles
d'un tableau s entre les bornes start et end est :
p=(end-start+1)/o
DO i=1,p-1
DO j=start,end,p
s(j+i)=s(j+i)+s(j+i-1)
END DO
END DO
DO i=start+p,end,p
DO j=p-1,0,-1
s(i+j)=s(i+j)+s(i-1)
END DO
END DO
La boucle de pas -1 dans le second nid permet de ne pas introduire
de bulle dans le pipeline. Ce code est du, en grande partie, au
professeur C. Timsit du laboratoire PRiSM.
Les chercheurs de l'université de Carnegie Mellon ont mis au point
une technique plus performante pour implanter les scans [13].
Cette technique du ``loop raking'' réduit le trafic mémoire.
L'un des auteurs Marco Zagha reconnaît que pour le Cray Y-MP, le
``loop raking'' n'apporte pas d'amélioration notable. Effectivement,
leur implantation en Fortran du calcul des sommes partielles n'est pas
plus rapide que la notre. Par contre leur implantation en C et assembleur
présente une accélération de 2 par rapport à la version Fortran.
Les temps d'exécution pour un test de calcul de sommes partielles que nous
avons effectué sur le Cray Y-MP du Centre de Calcul de l'université
Pierre et Marie Curie sont résumés dans le tableau ci-dessous.
| Méthode utilisée |
Temps d'exécution |
| Séquentielle |
0.35s |
| Partitionnement |
0.17s |
| Bibliothèque BLAS1 |
0.11s |
| ``loop raking'' en C |
0.09s |
Les résultats peuvent être considérés comme asymptotiques
puisque le vecteur traité comporte un million de composantes.
Au vu de ces résultats nous avons implantés les scans par
la méthode du partitionnement en gardant en mémoire que les
temps d'exécutions pouvaient être divisés par deux en
utilisant le langage C et l'assembleur du Cray.
| 15.2 |
Premier exemple : Évaluation d'un polynôme complexe |
|
L'évaluation d'un polynôme complexe se fait en deux étapes.
La première étape calcule les puissances du point complexe
(xRe,xIm) en lequel est évalué le polynôme :
yRe(1)=1.0
yIm(1)=0.0
DO i=2,n
tRe=yRe(i-1) (v1)
tIm=yIm(i-1) (v2)
yRe(i)=tRe*xRe-tIm*xIm (v3)
yIm(i)=tRe*xIm+tIm*xRe (v4)
END DO
La seconde étape consiste à effectuer un produit scalaire entre
ces puissances et les coefficients du polynôme.
tRe=aRe(1) (v5)
tIm=aIm(1) (v6)
DO i=2,n
tRe=tRe+yRe(i)*aRe(i)-yIm(i)*aIm(i) (v7)
tIm=tIm+yRe(i)*aIm(i)+yIm(i)*aRe(i) (v8)
END DO
La seconde section du code produit un système d'équations
normalisé. Ce n'est pas le cas de la première section.
Malheureusement, il s'agit d'un système irréductible.
Il est seulement possible, à l'aide de substitutions de réduire
le nombre d'équations à 2 :
v3 : { i | 2 <= i <= n } of real ;
v4 : { i | 2 <= i <= n } of real ;
v3[i] = case
{ i | i=2 } : 1.0 * xRe[i] - 0.0 * xIm[i] ;
{ i | i>2 } : v3[i-1] * xRe[i] - v4[i-1] * xIm[i] ;
esac ;
v4[i] = case
{ i | i=2 } : 1.0 * xIm[i] - 0.0 * xRe[i] ;
{ i | i>2 } : v3[i-1] * xIm[i] + v4[i-1] * xRe[i] ;
esac ;
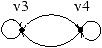
Le graphe de ce système est :
tous ses cycles ne passent pas par le même sommet.
Par contre les équations v3 et v4 possèdent
le même domaine de définition, il est facile de les fusionner.
Le système devient :
v3 : { i | 2 <= i <= n } of real x real ;
v3[i] = case
{ i | i=2 } :
( 1.0*xRe[i]-0.0*xIm[i] ) x ( 1.0*xIm[i]-0.0*xRe[i] ) ;
{ i | i>2 } :
( proj(v3,1)[i-1]*xRe[i] - proj(v3,2)[i-1]*xIm[i] ) x
( proj(v3,1)[i-1]*xIm[i] + proj(v3,1)[i-1]*xRe[i] ) ;
esac ;
Rappelons que nous notons x l'opérateur qui forme des couples
à partir de scalaires. De plus proj représente l'opérateur
de projection qui associe à un tuple et à une coordonnée la
composante du tuple correspondant à la coordonnée.
Le système se prête alors complètement à la détection des
scans. Le système après la détection est :
v3 : { i | 2 <= i <= n } of real x real ;
v7 : { i | 2 <= i <= n } of real ;
v8 : { i | 2 <= i <= n } of real ;
v3[i] = case
{ i | i=2 } :
( 1.0*xRe[i]-0.0*xIm[i] ) x ( 1.0*xIm[i]-0.0*xRe[i] ) ;
{ i | i>2 } :
Scan( { i' | 2<=i'<=n }, ([1]), *, xRe[i'] x xIm[i'], v3[i'] ) ;
esac ;
v7[i] = case
{ i | i=2 } :
aRe[1]+aRe[i]*proj(v3,1)[i]-aIm[i]*proj(v3,2)[i] ;
{ i | i>2 } :
Scan( { i' | 2<=i'<=n }, ([1]), +,
aRe[i']*proj(v3,1)[i']-aIm[i']*proj(v3,2)[i'], v7[i'] ) ;
esac ;
v8[i] = case
{ i | i=2 } :
aRe[1]+aIm[i]*proj(v3,1)[i]+aRe[i]*proj(v3,2)[i] ;
{ i | i>2 } :
Scan( { i' | 2<=i'<=n }, ( [1] ), +,
aIm[i']*proj(v3,1)[i']+aRe[i']*proj(v3,2)[i'], v8[i'] ) ;
esac ;
Dans ce système, les complexes sont considérés comme des couples
de réels (e.g. le couple xRe[i'] x xIm[i'] représente le complexe
xRe[i']+xIm[i'].i).
Les bases de temps du système sont facile à trouver :
|
|
| q(v3.0)=1 |
q(v2.1)=2 |
| q(v7.0)=2 |
q(v3.1)=3 |
| q(v8.0)=2 |
q(v3.1)=3 |
|
.
|
DO t=1,3
IF (t.EQ.1) THEN
v3(2)=COMPLX(xRe,xIm)
END IF
IF (t.EQ.2) THEN
t1(2:n)=COMPLX(xRe,xIm)
v3(2:n)=PRODUCT_PREFIX(temp1(2:n))
v7(2)=aRe(1)+aRe(2)*REAL(v3(2))-aIm(1)*AIMAG(v3(2))
v8(2)=aIm(1)+aIm(2)*REAL(v3(2))+aRe(1)*AIMAG(v3(2))
END IF
IF (t.EQ.3) THEN
t2(2)=v7(2)
t2(3:n)=REAL(v3(3:n))*aRe(3:n)-AIMAG(v3(3:n))*aIm(3:n)
v7(2:n)=SUM_PREFIX(t2(2:n))
t2(2)=ins6(2)
t2(3:n)=REAL(v3(3:n))*aIm(3:n)+AIMAG(v3(3:n))*aRe(3:n)
v8(2:n)=SUM_PREFIX(temp2(2:n))
END IF
END DO
Les calculs de réductions et de scans sont exprimés en utilisant
une version simplifiée des primitives de HPF. Dans la suite du
programme seuls v7(n) et v8(n) sont utilisés.
En conséquence des SUM_SCATTER doivent être utilisé
au lieu des SUM_PREFIX (il s'agit d'un code asap).
Les résultats de nos tests sont subsumés dans le tableau
des accélérations ci-dessous :
| Version \ degré |
100 |
1000 |
104 |
105 |
| Vectoriel (Cray) |
2.2 |
2.6 |
2.7 |
2.8 |
| Vectoriel (détecteur) |
0.7 |
2.8 |
3.6 |
3.8 |
| Vectoriel (assembleur) |
0.9 |
3.0 |
4.6 |
5.0 |
| Vectoriel et parallèle |
- |
2.0 |
8.1 |
10.2 |
Les accélérations sont toutes calculées par rapport au
programme initial compilé en forçant le compilateur du
Cray à générer du code séquentiel. La première ligne
montre que le compilateur du Cray
1
est déjà capable de
détection de réductions (a priori par une reconnaissance
de forme assez brutale). En fait les deux dernières sommes
sont reconnues. Notre code vectoriel se comporte mal avec des
petites valeurs du degré du polynôme, mais il est meilleur
asymptotiquement car le scan relatif à la multiplication
complexe a été détecté. Le code vectoriel dit assembleur
est calculé en analysant les temps passés dans chaque
procédure et en divisant par deux ceux concernant nos
procédures de calcul de scan. Nous avons vu que c'est
l'accélération du au passage en code assembleur.
Enfin la dernière ligne montre les temps obtenus en
utilisant des procédures de scan à la fois vectorisées
et parallélisées sur les 4 processeurs du Cray. La
parallélisation ne concerne pas que ces procédures ce qui
explique les bons résultats (en particulier, les boucles
sur les temporaires sont elles aussi parallélisées).
| 15.3 |
Second exemple : Un calcul de points selle |
|
Le calcul d'un point selle permet de rechercher les cols
des montagnes à partir d'une carte des élévations
(l'exemple est tiré d'un livre de référence pour
Fortran 77 [54]).
Il s'agit de trouver les points d'une matrice de nombres qui
sont à la fois le maximum de leur colonne et le minimum
de leur ligne (ou inversement).
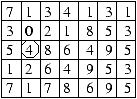
Par exemple dans la matrice ci-dessous :
le point encerclé est un point selle.
L'implantation de la recherche des points selle consiste
à calculer :
-
pour chaque ligne, le numéro de colonne de son plus petit et
de son plus grand élément ;
- pour chaque colonne, le numéro de ligne des deux éléments
extrêmes.
Une manière de procéder est donné dans l'extrait de programme
ci-dessous.
DO i=1,n
DO j=1,n
colmax=field(n+1,j) (v1)
...
IF (field(i,j).GT.colmax) THEN
field(n+1,j)=field(i,j) (v2)
field(n+3,j)=i (v3)
END IF
...
END DO
END DO
Seul le code calculant les numéros de lignes des maximums des
colonnes est explicité. Les autres calculs sont semblables.
Les extremums et les indices de ces extremums sont stockés
dans les quatre dernières lignes et dans les quatre dernières
colonnes du tableau.
Après une détection des récurrences nous obtenons le système
suivant.
field : { i,j | 1<=i<=n, 1<=j<=n } of real ;
v2 : { i,j | 1<=i<=n, 1<=j<=n } of real ;
v3 : { i,j | 1<=i<=n, 1<=j<=n } of real ;
v2[i,j] = case
{ i,j | i=1 } : if ( field[1,j] > field[n+1,j] )
then field[1,j] else field[n+1,j] ;
{ i,j | i>1 } : Scan( {i',j' | 1<=i'<=n, 1<=j'<=n}, ([1 0]),
max, field[i',j'], v2[i',j'] ) ;
esac ;
v3[i,j] = case
{ i,j | i=1 } : if ( field[1,j] > field[n+1,j] )
then 1 else field[n+3,j] ;
{ i,j | i>1 } : proj(
Scan( {i',j' | 1<=i'<=n, 1<=j'<=n}, ([1 0]),
search,
( field[i',j'] > v2[i'-1,j'] ) x i',
( field[i',j'] > field[n+3,j'] ) x 1 ),
2 ) ;
esac ;
Le if-then-else qui apparaît dans l'expression des équations
représente une expression conditionnelle de même sémantique que
le b?t:f du langage C.
Notons que l'opérateur Scan de v2 décrit des scans car toutes
ses valeurs sont utilisées par v3 alors que l'opérateur Scan
de v3 décrit des réductions car seule une valeur par ligne
d'accumulation est utilisée.
Les bases de temps de ce système sont triviales :
|
|
| q(v2.0)=1 |
q(v2.1)=2 |
| q(v3.0)=1 |
q(v3.1)=3 |
|
.
|
DO j=1,3
...
IF (t.EQ.1) THEN
v2(1,1:n)=MAX(field(1,1:n),field(n+1,1:n))
DO ALL j=1,n
IF ((field(1,j).GT.field(n+1,j)) THEN
v3(1,j)=1
ELSE
v3(1,j)=field(n+3,j)
END IF
END DO
END IF
IF (t.EQ.2) THEN
DO ALL j=1,n
t1(1)=v2(1,j)
t1(2:n)=field(2:n,j)
v2(1:n,j)=MAXVAL_PREFIX(t1(1:n))
END DO
END IF
IF (t.EQ.3) THEN
DO ALL j=1,n
t2(1)=v2(1,j)
t2(2:n)=field(2:n,j).GT.v2(1:n-1,j)
t3(1)=1
DO ALL index=2,n
t3(index)=index
END DO
v3(1:n,j)=SEL_PREFIX(t2(1:n),t3(1:n))
END DO
END IF
...
END DO
Comme les seuls éléments du tableau v3 qui sont utilisés
dans la suite du programme sont les v3(n,j), la dernière
instruction d'affectation peut être simplifiée :
v3(n,j)=SEL_SCATTER(t2(1:n),t3(1:n))
Les résultats des tests sont donnés dans le tableau suivant :
| Version \ n |
1000 |
4000 |
| Vectoriel (détecteur) |
1.5 |
1.8 |
| Vectoriel (assembleur) |
1.9 |
2.2 |
| Vectoriel et parallèle |
1.3 |
1.8 |
Le compilateur de Cray n'a pas réussi à détecter de réduction
dans le programme initial (soit à cause des IF, soit à cause
de l'utilisation des dernières lignes et colonnes du tableau des
élévations pour stocker les résultats des calculs).
En théorie une accélération de 2 peut être obtenue avec notre
code vectoriel. C'est assez encourageant dans la mesure ou un calcul de
scan en parallèle nécessite au moins 2 fois plus d'opérations
qu'un scan séquentiel. Sachant qu'un processeur vectoriel d'un
Cray Y-MP peut accélérer jusqu'à 10 fois un programme
séquentiel, l'accélération maximale est de 5. L'accélération
obtenue n'est donc pas ridicule, sachant que des manipulations sur des
temporaires sont rajoutées. Paralléliser la procédure de calcul
des scans n'est pas bénéfique, c'est normal car les scans sont assez
courts (1000 à 4000 données).
Si seuls les maximums et minimums de chaque ligne et de chaque colonne
sont calculés (leurs positions étant inutiles), plus aucun scan n'est
nécessaire. Les performances du programme vectorisé s'envolent :
| Version \ n |
1000 |
4000 |
| Vectoriel (détecteur) |
6.8 |
7.9 |
- 1
- Nous avons utilisé le Cray Fortran version 5.0.