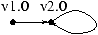| Chapter 11 |
Reconnaissance des réductions et des scans |
|
Les chapitres précédents décrivent comment normaliser un
système d'équations et comment représenter les scans détectés.
Ils peuvent être résumés dans
l'algorithme suivant :
Algorithme 8 Normalisation d'un système
-
Soit S un système SERA.
- Pour toutes les profondeurs p du système S en partant de
la plus grande jusqu'à 0 :
-
Calculer le graphe de S en ne tenant compte que
des dépendances de quasi-profondeur au moins égale à p.
- Trouver les composantes fortement connexes (CFCs) du graphe.
- Tenter de normaliser, par substitutions, les sous-systèmes
fortement connexes (en utilisant l'algorithme (7) par
exemple).
- Tenter de fusionner les équations des sous-systèmes
non normalisés à ce niveau.
-
Détecter les récurrences et les scans relatifs à des
dépendances de profondeur p et les réécrire avec un
opérateur Scan.
-
Tenter de promouvoir les opérateurs Scan en augmentant
leur nombre de directions.
-
Supprimer les dépendances inter-CFCs de quasi-profondeur
au moins égale à p (par substitution).
L'efficacité de l'algorithme peut être augmentée en choisissant
de construire le graphe des clauses plutôt que le graphe des équations.
Si la rapidité est primordiale, il est possible de ne considérer
que la profondeur 0. La normalisation risque de ne pas être très
efficace mais un seul calcul de graphe est nécessaire. L'étape
(7) permet de supprimer quelques arcs supplémentaires ;
l'implantation de cette étape ne présente pas de difficulté puisque
les CFCs sont connectées par un graphe sans circuit. D'un point de vue
sémantique, il s'agit de propagation de constantes entre les nids de
boucles.
Les phases (5) et (6) n'ont pas encore été
décrites ; elles font l'objet du présent chapitre. La phase (5)
consiste à réécrire les scans détectés à l'aide d'un opérateur Scan.
Seuls des opérateurs Scan uni-directionnels peuvent être introduits par cette
phase. C'est la phase (6) qui introduit des opérateurs
multi-directionnels. En fait elle n'introduit pas de nouvel opérateur mais
examine ceux déjà présents dans le système et augmente leur nombre de
vecteurs directeurs le cas échéant. Nous appelons ce procédé la
promotion d'un scan.
La phase (5) ne doit pas prendre en compte toutes les récurrences
mais uniquement les scans et les réductions.
Ces dernières présentent la particularité de pouvoir être calculées
par une fonction binaire associative. Donc il faut vérifier qu'il est
possible d'extraire de la définition de la récurrence une fonction
binaire associative. La section 10.3 montre, qu'actuellement, seule
une phase de reconnaissance de forme est adaptée pour résoudre ce
problème. Enfin, la dernière section présente un exemple complet de
détection d'une somme double.
| 11.1 |
Introduction de l'opérateur uni-directionnel |
|
Une fois le système d'équation normalisé ou partiellement
normalisé à la profondeur p (voir section 7.2),
la phase de détection proprement dite peut débuter.
La détection peut se faire, comme la normalisation, à
l'aide du graphe des équations ou à l'aide du graphe des
clauses. Quel que soit le graphe, seules les entités qui forment
une composante fortement connexe du graphe sont explorées.
Dans le cas du graphe des clauses, les expressions des clauses
sont explorées. Dans le cas du graphe des équations, toutes
les expressions des clauses de l'équation sont explorées.
Pour chaque expression, il est vérifié que :
-
l'expression contient une unique référence à la clause
elle-même (ou une unique référence de profondeur
supérieure ou égale à p dans le cas d'une normalisation
partielle) et cette référence correspond à une dépendance
uniforme (les paramètres de structure du programme sont
considérés comme étant des constantes) ;
- il est possible de tirer de l'expression une fonction binaire
associative.
Dans l'affirmative, l'expression de la clause (jusque là
une expression mathématique classique) est remplacée
par un opérateur Scan. La contrainte d'uniformité de la dépendance
peut être levée. Il est possible de calculer une récurrence
sur une trajectoire avec une distance variable entre deux points.
Le problème est qu'il devient nécessaire de modifier
l'opérateur Scan. Il devient plus complexe et une intéressante
propriété sur la transformation du domaine de la récurrence
(voir section 12.1.1) est perdue. Il est plus important
de conserver cette propriété que de prendre en compte des
récurrences aussi peu courantes.
Lorsque la détection se fait au niveau des équations,
il faut que les auto-références à l'équation dans le
texte de la clause soient, la plupart du temps, des
références à la clause elle-même.
Considérons le système suivant :
a : { i | 1 <= i <= n } of real ;
b : { i | 1 <= i <= n } of real ;
v : { i, j | 1 <= i <= n, 1 <= j <= 2 } of real ;
v[i,j] = case
{ i, j | j = 2 } : a[i] ;
{ i, j | i = 1, j = 1 } : b[1, 1] ;
{ i, j | i >= 2 , j = 1 } : v[i - 1, 2] + b[i] ;
esac
La troisième clause de l'équation v semble définir une
récurrence calculée suivant la première dimension. Ce n'est qu'une
illusion vu que la référence à v dans cette clause désigne
constamment la seconde clause de l'équation. D'ailleurs, si le graphe
des clauses a été choisi pour la détection, cette clause n'est pas
explorée puisqu'elle ne porte pas de boucle.
Pour vérifier que les références sont correctes, il faut
déterminer ce que signifie ``la plupart du temps''. En fait
le minimum est que la référence désigne au moins une fois
la clause explorée. Comme seules les dépendances uniformes
sont prises en compte, il suffit de vérifier que l'intersection
entre le domaine de la clause et ce même domaine translaté
du vecteur directeur -e des récurrences n'est pas vide.
Ce test assure que les récurrences calculent une suite d'au
moins deux termes. Il est possible d'être plus sélectif en
translatant le domaine de -k.e, avec k un entier positif
quelconque.
Notons c la clause explorée. Son domaine de définition est
Dc et son expression expc. Comme cette
clause ne contient qu'une référence à elle-même (ou que
les autres références peuvent être considérées comme
des constantes dans le cas d'une normalisation partielle) elle
peut s'écrire :
" z Î Dc, expc(z)=f(z,v(I(z)))
,
où v est le tableau multi-dimensionnel calculé par
l'équation contenant la clause. La fonction I est la
transformation d'indices de l'auto-référence à c.
Il est évident que si plusieurs auto-références
avec la même transformation I apparaissent dans la
clause elles comptent pour une seule.
Sous réserve que la fonction de propagation f puisse s'écrire
comme l zx.b(x,d(z)) avec b une fonction binaire associative
(voir section 10.3), la clause peut s'exprimer avec
un opérateur Scan :
" z Î Dc, expc(z)=
Scan( D,(e),b,d,g)(z)
,
avec les entités D, e et g définies comme suit :
-
le domaine d'accumulation D est l'enveloppe
convexe de l'union de Dc avec son image par la
translation de vecteur -e ;
- la direction e est calculée par la formule
z-I(z), le point z peut être choisi de façon
quelconque dans Dc puisque I est uniforme ;
- l'équation g est tout simplement une référence
au tableau v avec une transformation d'indices égale à
l'identité. Le domaine de définition de g est l'enveloppe
convexe de l'intersection de Dc avec son image par la
translation de vecteur -e.
-
Preuve:
-
Le tableau u calculé par l'opérateur est :
|
" zÎ D,
u(z)=
|
ì
ï
í
ï
î |
| si |
|
g(z) |
| sinon |
f(z,u(z-e))
. |
|
|
E={ z-l e | zÎ Dc, lÎ[0,1] }
.
Cet ensemble contient tous les éléments de Dc et de son
translaté par -e (il suffit de prendre l dans {0,1}).
L'ensemble E est convexe car il contient le milieu de deux
de ses éléments. En effet soient a et b ces éléments il existe
deux points z et z' de Dc et deux réels l et µ
dans [0,1] tels que :
a=z-l e et b=z'-µ e
.
Le milieu de a et b est :
Le milieu de z et z' est bien un point du convexe Dc et
l+µ/2 est bien un réel de [0,1].
En conséquence D est inclus dans E. De plus tout
point de E est un barycentre d'un z élément de
Dc et de z-e élément de l'image translatée. Donc
D est l'ensemble des points entiers de E.
Ce résultat est important car il assure que
mine D(z) avec zÎ Dc est
un élément de la translation de Dc par e.
D'après la définition de mine D c'est
forcément un point de la translation de Dc qui n'est
pas dans Dc. Donc Dc est inclus dans
D-mine D( Dc). Or sur
ce domaine u(z)=f(z,u(z-e)). Comme, de plus, sur
mine D( Dc) l'équation
d'initialisation est égale à v, il vient :
" zÎ Dc, u(z)=expc(z)
.
La détection de récurrences est limitée, ici, aux scans
et aux réductions mais il est tout à fait possible de
détecter une classe plus large de récurrences (ce que
font nos prototypes écrits en Lisp). Il suffit d'être plus
laxiste sur la forme de la fonction de propagation (pour sélectionner
des fonctions de propagation qui ne sont pas forcément binaires
et associatives)
et sur le nombre d'auto-références à la clause (pour détecter
des récurrences d'ordre supérieur à 1).
Nous allons montrer, à partir du programme ci-dessous, comment notre
méthode prend en compte les scans uni-directionnels.
x(0)=0 (v1)
DO i=1,2*n
save(i)=x(2*n-i+1) (v2)
x(i)=x(i-1)+save(i) (v3)
END DO
Le système automatiquement extrait de ce programme est
(voir la section 7.1.1 pour plus de détails) :
v1 : real ;
v2 : { i | 1 <= i <= 2*n } of real ;
v3 : { i | 1 <= i <= 2*n } of real ;
v1 = 0 ;
v2[i] = case
{ i | 1 <= i <= n } : x[2*n-i+1] ;
{ i | n+1 <= i <= 2*n } : v3[2*n-i+1] ;
esac ;
v3[i] = case
{ i | i = 1 } : v1 + v2[i] ;
{ i | i >= 2 } : v3[i-1] + v2[i] ;
esac ;
Pour cet exemple une normalisation moyennement efficace suffit.
Nous allons donc travailler sur le graphe des équations et
tenter une normalisation en une seule passe.
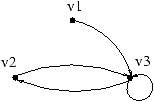
Le graphe des équations du système est :
Tous les circuits passent par v3, la normalisation par
substitutions va donc simplement consister à remplacer,
dans v3 les références à v1 et v2
par les expressions de ces équations.
v3 : { i | 1 <= i <= 2*n } of real ;
v3[i] = case
{ i | i=1 } : 0 + x[2*n-i+1] ;
{ i | 2<=i<=n } : v3[i-1] + x[2*n-i+1] ;
{ i | n+1<=i<=2*n } : v3[i-1] + v3[2*n-i+1] ;
esac ;
Ce système est fatalement normalisé puisqu'il ne contient plus
qu'une seule équation. La détection des scans, par simple examen
des clauses, peut être appliquée. La première clause ne contient
pas d'auto-référence ; elle est éliminée. La seconde contient
une unique référence à elle-même (i.e. à v3.1).
De plus une fonction binaire et associative peut être extraite de
la fonction de propagation : l'addition. La clause est donc bien un
scan. La dernière clause aussi car elle contient une auto-référence
(i.e. v3[i-1] référence v3.2) et une référence à une
autre clause (i.e. v3[2*n-i+1] référence v3.1).
Le système après introduction des opérateurs Scan s'écrit :
v3 : { i | 1 <= i <= 2*n } of real ;
v3[i] = case
{ i | i=1 } : 0 + x[2*n-i+1] ;
{ i | 2<=i<=n } : Scan( { i' | 1<=i'<=n }, ( [1] ),
+, x[2*n-i'+1], v3 )[i] ;
{ i | n+1<=i<=2*n } : Scan( { i' | n<=i'<=2*n }, ( [1] ),
+, v3[2*n-i'+1], v3 )[i] ;
esac ;
Si ce résultat est transcrit en utilisant les notations standards
(la transcription est manuelle mais pourrait facilement être
automatisée), nous constatons que le programme calcule une somme
pondérée :
|
v3 |
(2n)= |
|
((n-i+2)×x(2n-i+1))
.
|
| 11.2 |
Introduction de l'opérateur multi-directionnel |
|
L'opérateur uni-directionnel décrit un ensemble de scans
calculés selon une droite dans l'espace d'accumulation.
Certains scans sont calculés suivant une ligne brisée,
c'est-à-dire suivant plusieurs directions.
L'archétype de ces récurrences est la somme des éléments
d'une matrice a. Une telle somme est implantée,
en séquentiel, par quelques lignes :
s=0
DO i=1,n
DO j=1,n
s=s+a(i,j)
END DO
END DO
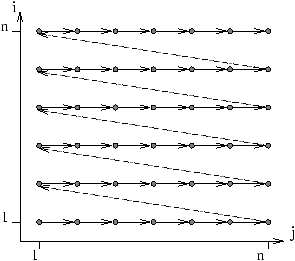
Le graphe de dépendance de ce programme montre que la réduction
est calculée suivant une ligne brisée dans l'espace d'accumulation :
Il est remarquable que cette ligne brisée est principalement constituée
des droites (en traits pleins) suivant lesquelles sont calculées les
réductions de la boucle interne. Ces droites sont reliées par des arcs
(en traits pointillés) représentant les dépendances entre le résultat
d'une réduction interne et la valeur initiale de la réduction suivante.
Il est toujours préférable d'obtenir des récurrences
multi-directionnelles lorsque c'est possible. Calculer une
seule récurrence portant sur un grand nombre de données
est plus efficace que calculer une série de récurrences
portant sur un petit nombre de données (voir section
11.2).
La détection de scans multi-directionnels n'a de sens que dans
le cadre d'une normalisation profondeur par profondeur.
Dans la suite de la section, il est supposé que le système
analysé a été normalisé pour la profondeur p.
L'introduction d'un opérateur multi-directionnel se fait par
examen des opérateurs déjà présents dans le système
d'équations. Pour un opérateur donné, il faut vérifier
que la valeur d'initialisation de chaque scan qu'il décrit
est une simple référence au résultat du scan précédent.
Décrivons plus formellement les conditions qu'un opérateur Scan
doit respecter pour donner lieu à un opérateur Scan avec un
nombre supérieur de directions.
L'opérateur s'écrit :
|
Scan( D |
,(ei) |
|
,b,d,g)° f
.
|
-
il constitue à lui seul l'expression de la clause c
(sinon il est impossible qu'il puisse se référencer directement) ;
- un nombre s' de clauses, compris entre 1 et
s-1, sont de la forme f(z,vc(Ij(z))) (la fonction
f est l zx.b(x,d(z)), vc désigne le tableau
multi-dimensionnel calculé par la clause c et Ij
est une fonction d'indices dénotant une dépendance de
profondeur p) :
- une nouvelle direction e0 doit pouvoir être extraite de ces
s' clauses ;
- l'union des domaines des autres clauses de g doit correspondre
au domaine de l'équation d'initialisation du nouvel opérateur.
C'est à dire, en supposant que les s' premières clauses de g
sont celles décrites plus haut :
Trouver une nouvelle direction e0 des récurrences consiste
à résoudre le problème en nombres entiers ci-dessous :
|
|
|
| " jÎ Ns'*, " zÎ Djg,
max |
|
(z-e0)=f(Ij(z)) |
|
|
|
-
Preuve:
-
Pour prouver cette affirmation, il faut revenir à la définition
de l'opérateur Scan. La récurrence de la clause c (sans tenir
compte de la transformation f) calcule le tableau
multi-dimensionnel v suivant :
|
" zÎ D,
v(z)=
|
ì
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
î |
| si |
|
g(z) |
| sinon si |
|
|
| ... |
| sinon si |
|
|
| sinon |
f(z,v(z-ek))
. |
|
|
|
|
ì
ï
ï
í
ï
ï
î |
|
si |
|
g'(z) |
|
sinon si |
|
f(z,vc(Ij(z)))
. |
|
|
" zÎ Dc, vc(z)=v(f(z))
,
d'où
|
" zÎ Ij-1( Dc), vc(Ij(z))=v(f(Ij(z)))
=v(max |
|
(z-e0))
.
|
|
Scan( D |
,(ei) |
|
,b,d,g')° f
.
|
Pratiquement le problème (10.1) peut être résolu
par le logiciel PIP. En effet calculer
revient à chercher le vecteur
l=(l1,...,lk)
lexicographiquement positif et maximum tel que
Le problème (10.1) se résume donc à trouver le minimum
lexicographique du vecteur (|e0|,-l) sous les contraintes
|
|
| l>0 |
|
" jÎN |
s*, z-e0+ |
|
li ei=f(Ij(z))
. |
|
|
La nouvelle manière (par rapport à [55])
d'introduire les opérateurs Scan uni-directionnels avec
un domaine d'accumulation D comportant le domaine
des valeurs initiales permet la promotion des opérateurs
Scan (i.e. l'augmentation de leurs nombres de directions)
sans recourir à l'élargissement du domaine D.
Encore plus important, il n'est plus utile d'avoir recours
à des opérateurs Scan emboîtés, ce qui simplifie
la représentation des systèmes d'équations.
| 11.3 |
Extraction des fonctions associatives |
|
Le premier critère pour reconnaître une réduction ou un scan est
de vérifier que la récurrence est bien d'ordre 1 (ou peut
être transformée en récurrence d'ordre 1, par exemple en
utilisant des opérations sur les matrices).
Il faut ensuite procéder en deux étapes : extraire
une fonction binaire de l'expression de la récurrence puis
vérifier que cette fonction est bien associative.
Notons l zx.f(z,x) la fonction de propagation de la récurrence.
Dans cette notation z représente le vecteur d'itération courant et
x la valeur précédente dans la suite que calcule la récurrence.
L'extraction d'une fonction binaire de cette fonction de propagation
consiste à trouver une fonction b et une suite de valeurs
(d(z))zÎ D telles que :
$ f' telle que " zÎ D, " x, f'(d(z),x)=f(z,x)
,
et
f'(d(z1),f'(d(z0),x))=f'(b(d(z0),d(z1)),x)
( D est l'espace d'accumulation de la récurrence).
Cette fonction b est connue sous le nom de fonction compagnon
(voir [38]). Pour trouver la fonction binaire et la suite
de valeurs une reconnaissance de forme n'est pas adaptée. En effet
la reconnaissance échoue la plupart du temps car l'appariement
doit être fait sur un plan sémantique. Il a été montré
qu'une simple vue syntaxique n'est pas suffisante (cf [24]).
Une manière d'extraire automatiquement des fonctions binaires
serait de mettre au point un système de réécriture capable de
transformer des expressions du type f'(d(z1),f'(d(z0),x)) en des
expressions du type f'(b(d(z0),d(z1)),x). Les règles de
réécriture à utiliser sont les règles usuelles sur les
opérateurs de base en informatique
(e.g. additions, multiplication et expressions conditionnelles).
Il n'existe pas de critère précis permettant
de choisir les bonnes règles à appliquer. De plus il est hors
de question d'essayer toutes les combinaisons possibles.
La méthode théorique est cependant applicable par un humain.
Considérons, par exemple, une fonction générique de recherche
d'un élément particulier dans un tableau :
|
l ix. |
| case |
| |
a(i) |
® |
b(i) |
| |
¬ a(i) |
® |
x |
| esac , |
|
|
f'(d,x)= |
| case |
| |
d[1] |
® |
d[2] |
| |
¬ d[1] |
® |
x |
| esac . |
|
|
f'(di,f'(di-1,x))= |
| case |
| |
di[1] |
® |
di[2] |
| |
¬ di[1] Ù di-1[1] |
® |
di-1[2] |
| |
¬ di[1] Ù ¬ di-1[1] |
® |
x |
| esac , |
|
|
f'(b(di-1,di),x)= |
| case |
| |
b(di-1,di)[1] |
® |
b(di-1,di)[2] |
| |
¬ b(di-1,di)[1] |
® |
x |
| esac . |
|
|
" (di-1,di), b(di-1,di)=
|
æ
ç
ç
ç
è |
|
| di-1[1]Ú di[1],
|
ì
ï
í
ï
î |
| case |
| |
di[1] |
® |
di[2] |
| |
¬ di[1] |
® |
di-1[2] |
| esac |
|
|
ü
ï
ý
ï
þ |
|
|
|
ö
÷
÷
÷
ø |
L'exemple précédent montre que l'automatisation de l'extraction de
la fonction binaire est, sinon impossible, du moins extrêmement
difficile. La phase de vérification de l'associativité de la fonction
binaire n'est pas moins complexe (voir [36]). Seul un système
expert est susceptible de résoudre ce problème.
La fonction search est associative. Pour prouver ceci il faudrait que
le système expert sache que deux instructions conditionnelles
emboîtées donnent une autre instruction conditionnelle.
Ensuite, il lui faudrait simplifier (en un sens difficile à déterminer)
les différents cas pour montrer l'associativité.
Grâce à la fonction binaire associative search, il est possible de
présenter le système trouvé par le détecteur de réductions et de
scans lorsqu'il est appliqué au test de l'Argonne décrit plus haut.
Dans ce programme Alpha, il est supposé que N est l'ensemble
des nombres naturels à partir de 1. Il est rappelé que x est
un opérateur qui forme des couples à partir de deux vecteurs de
scalaires et que proj est un opérateur de projection.
b : { i | 1 <= i <= n } of real ;
v2 : { i | 1 <= i <= n } of real ;
v4 : real ;
v5 : real ;
v2[i] = Scan( { i' | 0<=i'<=n }, ( [1] ), max, b[i'], x )[i] ;
v4 = v2[n] ;
v5 = proj( Scan( { i' | 0<=i'<=n }, ( [1] ), search, ( b > v2 ) x N,
true x 0 )[n], 2 ) ;
Aussi, la méthode la plus efficace pour reconnaître les réductions
et les scans est encore de choisir un ensemble d'expressions génériques
caractérisant les plus utiles de ces récurrences. Une simple
reconnaissance de formes suffit alors pour extraire la fonction
binaire associative.
Nous nous limitons, pour l'instant, à la détection des réductions
et des scans simples. C'est à dire ceux qui peuvent être implantés
directement sur une machine parallèle (ce sont les plus couramment
utilisés). Nos prototypes savent reconnaître les expressions
génériques à base d'addition, de multiplication, de maximum,
de minimum, de OU logique, de ET logique et d'égalité logique.
Les expressions à base de fonction search sont aussi prises en compte.
En effet ces fonctions peuvent être implantées en utilisant un
calcul de maximum.
Une phase de normalisation des expressions est souhaitable pour
une plus grande efficacité. Cette phase n'est pas particulière à
notre méthode. La méthode basée sur l'évaluation symbolique
nécessite aussi une simplification des valeurs symboliques finales.
Par exemple, les propriétés de commutativité et d'associativité
de l'opérateur d'addition sont utilisées pour normaliser
l'expression (a(i)+x)-b(i) en l'expression x+(a(i)-b(i)). Ainsi seule
une expression générique x+exp est nécessaire.
Pour les expressions à base d'additions et de multiplications, il suffit
de considérer cette expression comme un polynôme et de normaliser le
polynôme. Il est plus difficile de normaliser les expressions à base
d'extrema et d'expressions conditionnelles. Nous nous limitons à
supprimer les constantes booléennes .TRUE. et .FALSE..
Lorsque le couple fonction binaire et données exprime une récurrence
triviale, l'opérateur Scan correspondant n'est pas généré, la
récurrence est directement résolue.
Par exemple le programme ci-dessous définit une récurrence
triviale.
a(0)=0 (v1)
DO i=1,n
a(i)=a(i-1) (v2)
END DO
Plutôt que de générer un système avec un opérateur Scan
v1 : real ;
v2 : { i | 1 <= i <= n } of real ;
v1 = 0 ;
v2 = case
{ i | i = 1 } : v1 ;
{ i | i >= 2 } : Scan( { i' | 0<=i'<=n }, ( [1] ), +, 0, v1 )[i] ;
esac ;
il est préférable de remplacer directement la récurrence par
l'expression de sa solution ;
v1 : real ;
v2 : { i | 1 <= i <= n } of real ;
v1 = 0 ;
v2 = case
{ i | i = 1 } : v1 ;
{ i | i >= 2 } : v1 ;
esac ;
Cet exemple n'est pas correctement traité par la méthode
géométrique ; une analyse stricte des dépendances conduit
à un code séquentiel. Par contre, toutes les méthodes de
détection des réductions parviennent à traiter cet exemple.
Ce n'est plus le cas si l'exemple se complexifie un peu :
DO i=1,n
DO j=1,n
a(i,j)=a(i,0) (v1)
IF (i.EQ.j) THEN
a(i,i)=a(i-1,i-1) (v2)
END IF
END DO
END DO
L'effet de ce programme est d'initialiser chaque ligne de la
matrice avec la valeur de la colonne 0, sauf pour la diagonale
qui est initialisée avec la valeur a(0,0).
Avec notre méthode de détection le système final est :
v1 : { i,j | 1<=i<=n, 1<=j<=n } of real ;
v2 : { i,j | 1<=i<=n, j=i } of real ;
v1[i,j] = a[i,0] ;
v2[i,j] = a[0,0] ;
Une méthode basée sur l'évaluation symbolique n'essayera
pas de détecter de réduction dans la boucle sur j
à cause des dépendances complexes entre les éléments
du tableau a.
Notre prototype Lisp résoud aussi les suites
arithmétiques et géométriques (voir le test en A.2.7).
Notre phase de reconnaissance de formes est vraiment très réduite
comme le montre la concision de la base de règles du prototype :
(defvar #:red:rules (list
(#:pm:makeRule
'(reference recur)
'( ( reference ) recur reference )
'#:red:propag)
(#:pm:makeRule
'(reference op exp1 exp2 recur)
'( ( reference ) recur ( op exp1 exp2 ) )
'#:red:associative)
(#:pm:makeRule
'(reference exp1 exp2 recur)
'( ( reference ) recur (multaddform reference exp1 exp2))
'#:red:multAddForm)
(#:pm:makeRule
'(reference condition exp1 exp2 recur)
'( ( reference ) recur (if condition exp1 exp2))
'#:red:select)
(#:pm:makeRule
'(reference1 reference2 exp recur)
'( ( reference1 reference2 ) recur exp)
'#:red:sndOrder)
))
La première règle traite les cas triviaux d'initialisation de
tableaux avec une valeur propagée. La seconde traite les fonctions
de propagation déjà exprimées avec un opérateur binaire.
La troisième règle traite les fonctions de propagation de
la forme a(i)*x+b(i) où x est la valeur précédente de
la récurrence (pour l'instant seules les récurrences de ce type
qui peuvent être résolues sont traitées). La quatrième
règle traite les fonctions de propagation à base d'expressions
conditionnelles. Enfin la dernière règle est prévue pour
les récurrences d'ordre 2, pour l'instant seules les récurrences
triviales sont prises en compte.
Pour résumer, nous donnons l'algorithme d'extraction des fonctions
binaires et associatives.
Algorithme 9 Extraction des scans et des réductions
-
Soit une fonction de propagation f(z,x) où z est le vecteur
d'itération courant et x la valeur précédente de la récurrence.
- Normaliser la fonction f :
-
si f ne comporte que des opérations + et *,
utiliser une normalisation de polynômes ;
- si f comporte des instructions conditionnelles, simplifier
les instructions conditionnelles emboîtées ;
- dans les autres cas considérer les expressions non linéaires
comme des variables et appliquer la normalisation sur les polynômes.
- Appliquer la reconnaissance de forme à la fonction normalisée.
- Retourner :
-
soit, directement la solution de la récurrence ;
- soit, si elles existent, la fonction binaire b et la suite
de valeurs d associée ;
- soit, une valeur spéciale pour indiquer que la récurrence
n'est ni triviale, ni un scan.
Cet algorithme est appelé lors de l'introduction de l'opérateur
Scan uni-directionnel, c'est-à-dire au niveau de l'étape (5)
de l'algorithme (8) (voir le chapitre 10).
| 11.4 |
Améliorations de la reconnaissance de forme |
|
La phase de reconnaissance des scans et des réductions peut être
améliorée. Pour cela il faut affiner la phase de normalisation
des expressions et augmenter le nombre de formes à reconnaître
(il s'agit d'ajouter un petit nombre de cas).
En ce qui concerne la normalisation, le déroulement des expressions
peut conduire à reconnaître plus de scans.
Ainsi la récurrence ci-dessous
a : { i | 1 <= i <= n } of real ;
v : { i | 1 <= i <= n } of real ;
v[i] = case
{ i | i = 0 } : a[0] ;
{ i | i >= 1 } : a[i] / v[i-1] ;
esac ;
peut s'écrire :
a : { i | 1 <= i <= n } of real ;
v : { i | 1 <= i <= n } of real ;
v[i] = case
{ i | i = 0 } : a[0] ;
{ i | i = 1 } : a[1] / a[0] ;
{ i | i >= 2 } : ( a[i] / a[i-1] ) * v[i-2] ;
esac ;
ce qui définit deux scans simples qui calculent le produit
des éléments d'un vecteur.
Il serait aussi utile de prendre en compte des récurrences avec une
fonction de propagation plus complexe. Par exemple la normalisation de
récurrences définies par deux équations conduit souvent à des
récurrences de la forme :
a : { i | 1 <= i <= n } of real ;
v : { i | 1 <= i <= n } of real ;
v[i] = case
{ i | i = 0 } : cst ;
{ i | i >= 1 } : a[i] * v[i-1] + b[i];
esac ;
Ces récurrences peuvent être implantées efficacement sur des machines
parallèles (voir [39]). Elles ne sont pas prises en compte
par nos prototypes pour l'instant, mais il suffit de rajouter une
expression générique.
Certaines récurrences sont des réductions ou des scans dont la fonction
binaire associative opère sur des matrices ; ce sont des récurrences
d'ordre n>1 avec des fonctions de propagation affines.
Pour exploiter ces récurrences il suffirait de :
-
permettre l'introduction d'un opérateur Scan lorsqu'une clause
comporte plusieurs auto-références (autant que l'ordre de la récurrence,
voir 10.1) ;
- prévoir des règles d'extraction de fonctions binaires pour ces
récurrences, c'est-à-dire des fonctions opérant sur des matrices.
Le second point peut être réalisé efficacement, en évitant les
calculs superflus (opération décrite dans [39]).
| 11.5 |
Exemple de détection de réduction |
|
Pour résumer cette partie nous illustrons, sur un exemple,
les différentes étapes de notre méthode de détection
des récurrences (i.e. des scans et des réductions).
L'exemple est un programme calculant la somme des éléments
d'une matrice :
s=0 (v1)
DO i=1,n
DO j=1,i
s=s+a(i,j) (v2)
END DO
END DO
Cet algorithme est utilisé dans [29] comme exemple de
code impossible à paralléliser par les méthodes classiques.
La première étape consiste à mettre le programme sous
la forme d'un système d'équations. La variable scalaire s
est expansée en tableau à deux dimensions puisqu'il y a deux
boucles englobantes. La référence à s dans le membre droit
de v2 est remplacée par ses trois sources possibles.
a : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v1 : real ;
v2 : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v1 = 0 ;
v2[i,j] =
case
{ i,j | j>1 } : v2[i,j-1] + a[i,j] ;
{ i,j | i>1, j=1 } : v2[i-1,i-1] + a[i,j] ;
{ i,j | i=1, j=1 } : v1 + a[i,j] ;
esac ;
Il s'agit maintenant de normaliser le système d'équation. Nous adoptons
le schéma efficace, c'est-à-dire que nous commençons par normaliser
le système pour la profondeur 1. Pour plus de précision nous allons
travailler sur le graphe des clauses et non pas sur celui des équations.
Il existe trois dépendances de quasi-profondeur 1, la dépendance de
v2.0 (la première clause de v2) sur elle-même et les
dépendances de v2.0 envers v2.1 et v2.2.
Ces trois dépendances possèdent la même transformation d'indices
(i,j -> i,j-1). le graphe des clauses pour cette profondeur est :
Ce graphe est normalisé. Il est donc valide d'introduire l'opérateur
de récurrence uni-directionnel pour la première clause de v2.
Le système devient :
a : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v1 : real ;
v2 : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v1 = 0 ;
v2[i,j] =
case
{ i,j | j>1 } : Scan( {i',j' | 1<=i'<=n, 1<=j'<=i'},
([0,1]), +, a[i',j'] , v2[i',j'] ) ;
{ i,j | i>1, j=1 } : v2[i-1,i-1] + a[i,j] ;
{ i,j | i=1, j=1 } : v1 + a[i,j] ;
esac ;
Ce système ne comporte plus que deux dépendances de
quasi-profondeur 1, celles de l'équation d'initialisation
de l'opérateur Scan de la clause v2.0 envers les clauses
v2.1 et v2.2 :
Une phase de suppression des arcs inter-CFCs est effectuée.
Il en résulte que la référence à v2 dans l'équation
d'initialisation de l'opérateur Scan est remplacée par sa
valeur. De plus les clauses v2.1 et v2.2 ne sont plus
référencées donc sont supprimées.
a : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v1 : real ;
v2 : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v1 = 0 ;
v2[i] =
case
{ i,j | j>1 } :
Scan( { i',j' | 1<=i'<=n, 1<=j'<=i' }, ( [0,1] ), +, a[i',j'] ,
case
{ k,l | k>1, l=1 } : v2[k-1,k-1] + a[k,l] ;
{ k,l | k=1, l=1 } : v1 + a[k,l] ;
esac ; )
esac ;
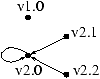
Ce nouveau système présente deux dépendances de
pseudo-profondeur 0, une de v2.0 sur elle-même
et une de cette même clause envers v1.0.
Le graphe des clauses associé est dessiné ci-dessous.
Il n'y a pas de circuit de longueur au moins 2, le graphe est normalisé.
L'introduction de nouveaux opérateurs uni-directionnels est tentée, mais
échoue.
Il faut alors essayer de promouvoir les opérateurs existants
en augmentant leur nombre de directions.
Pour le seul opérateur du système, le programme en nombres entiers
à résoudre est la minimisation du vecteur (|e0|,|e1|,-l)
sous les contraintes :
|
|
| l>0 |
| "
|
æ
è |
|
|
|
ö
ø |
Î { i',j' | i'>1, j'=1 },
|
æ
è |
|
|
|
ö
ø |
= |
æ
è |
|
|
|
ö
ø |
- |
æ
è |
|
|
|
ö
ø |
+ l. |
æ
è |
|
|
|
ö
ø |
. |
|
|
a : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v1 : real ;
v2 : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v1 = 0 ;
v2[i,j] =
case
{ i,j | j>1 } :
Scan( { i',j' | 1<=i'<=n, 1<=j'<=i' }, ( [1,0], [0,1] ), +, a[i',j'] ,
v1 + a[i',j'] ) ;
esac ;
Le graphe de ce système comporte encore un arc :
Le remplacement de v1 dans v2 par sa valeur donne le
système final :
a : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v2 : { i,j | 1<=i<=n, 1<=j<=i } of real ;
v2[i,j] =
case
{ i,j | j>1 } :
Scan( { i',j' | 1<=i'<=n, 1<=j'<=i' }, ( [1,0], [0,1] ), +, a[i',j'] ,
0 + a[1,1] ) ;
esac ;
En définitive, la double somme a été détectée car l'opérateur
Scan du système ci-dessus ne calcule rien d'autre que :
Le code parallèle est donc réduit à un appel à une primitive
optimisée de calcul de scan (ici de réduction puisque seule la
dernière valeur du scan est utilisée). Le temps d'exécution
est donc de l'ordre de n2/p+log2(p). Par les méthodes
classiques le code généré est séquentiel donc de l'ordre de n2.
Si seuls les scans concernant la boucle sur j sont détectés
(par exemple, en utilisant une méthode de détection de réductions
par évaluation symbolique), le temps d'exécution du programme
parallèle est de l'ordre de n(n/p+log2(p)). Ce temps
est même porté à n2/p+np, contre n2/p+p pour
notre méthode, si la primitive de scan n'utilise pas d'arbre binaire
de calcul pour la mise à jour des résultats partiels sur chaque
processeur.
Une remarque intéressante est que l'introduction de l'opérateur Scan
permet de vérifier que le programme calcule bien la somme des éléments
du tableau a. Une autre utilisation de notre détecteur de
récurrence serait de faire de la preuve de programmes.