Overview of the Method

2 Overview of the Method

2.1 What is a Reduction?

A reduction -- the name comes from the APL language [8] -- is any operation which takes a set of values as argument and gives a single value in return¹. Most often, a reduction is defined as the repeated application of a binary function to the elements of the input set in some order:

s = f(... f(a₁,a₂),..., a_n). (1)

Specially interesting is the case where f is an associative function. Commutativity and the existence of a unit are also useful. With the help of these properties, definition (1) can be rearranged in various ways in order to exhibit parallelism. As a rough estimate, reduction of n values on P processors takes about n/P + log₂ P units of time, excluding communication delays if any.

APL was the first language to introduce a specific notation for reduction. In contrast, many ordinary imperative languages, new and old, have no such feature. In Fortran, for instance, one has to write:

Program reduc
s = a(1)
do i = 2,n
  s = f(s,a(i))
end do
end

and the situation is similar for C or Pascal. With the advent of massively parallel computers, there is a strong incentive to extract the last ounce of parallelism from sequential programs, hence the importance of detecting associative reductions.

The reader must be warned that some computer operators are only approximately associative. For instance, addition of floating point numbers is associative up to rounding errors. While there is no reason to suppose that a parallel reduction is less precise than a sequential one [14], the user must be aware that a program to which reduction parallelization has been applied may not give exactly the same results as its sequential original. The extent of the difference depends on the numerical stability of the algorithm, and this question is beyond the scope of this paper.

2.2 Detecting a reduction

The question is thus to identify reductions when they are concealed in a sequential program.

It is not too difficult to identify code such as:

    do i = ...
      s = f(s)
    end do

The question is then whether the assignment may be rewritten as

      s = g(s, e(i))

with g an associative operation. This is a difficult mathematical question. Usually, the associativity of a binary operation has to be proved, and such a proof may be of arbitrary difficulty. Since it is not possible, at least with present technology, to include a theorem prover in a compiler, the obvious solution is to use a catalog of predefined reductions and to match this knowledge base against the object program. This is done in many commercial parallelizers, which are able to recognize elementary reductions like sums and dot products.

Such recognition of reductions by pattern matching is more complicated than it looks: consider for example the problem of summing the components of a vector. It may be written in many different ways, among which:

program A              program B                 program C
s = 0.                 s = a(1)             1    s = 0.
do i = 1,n             do i = 2,n                do i = 1,n
    s = s + a(i)           s = a(i) + s     2       t = s + a(i)
end do                 end do               3       s = t
end                    end                       end do
                                                 end

Furthermore, most of the time, the summation loop above will be encumbered by extraneous code, which may interfere -- or not -- with the summation. It would need a very large knowledge base to recognize all these forms as equivalent.

The first idea is to go beyond ``first order'' pattern matching as is found, e.g., in parsers or in such languages as ML. For instance, the best way of deciding whether a statement s = f(s) is a summation is to compute (with the help of a computer algebra system) the quantity f(s) - s and to test whether the result is independent of s or not. Similarly, the best way to handle extraneous code in the loop body is to analyze its dependence graph. We are thus lead to the use of ``matching functions'' of arbitrary complexity. The set of matching functions is the knowledge base of our reduction detector. It needs not be fixed for all times and circumstances. Special application fields may have their own type of reductions and associated matching functions. For all these reasons, it is impossible to combine the pattern matching functions into one grand pattern, as in done, for instance, in LR(k) parsers. Application of the several matching functions must be sequential, hence our insistence in having as few of them as possible.

As is well known, normalization of the object program is a powerful tool for reducing the size of the knowledge base. Ideally, all equivalent programs should transform into the same normal form and the reduction detection should be done on the normal form. This is clearly impossible, since it would give an algorithm for testing the equivalence of two programs, which is undecidable as soon as the programming language is powerful enough. The way out is both to restrict the input language -- to static control programs in our case -- and to accept imperfect normal forms, in which some but not all equivalent programs have the same normalization.

For instance, with the system which is described in this paper, program A and C normalize to the same form, but program B does not. This is as it should be, since program A and B are equivalent only if n ³ 1. But even adding this information will not enable us to have program A and B converge to the same normal form, unless we find a way for doing formal computations on reductions, a subject for future research.

Many researchers have defined normal forms for use in reduction detection and other program transformations. The best known one is obtained by symbolic execution [9]. When the presence of a reduction in a loop is suspected, its body is submitted to an algebraic interpreter. Consider for instance program C, and let s_i⁰, t_i⁰ be the values of s and t at the beginning of iteration i of the loop. Similarly, let s_i^k, t_i^k be the values of these variables after execution of statement k in iteration i. Symbolic interpretation of statement 2 and 3 gives successively:

t_i²	=	s_i⁰ + a(i)
s_i³	=	s_i⁰ + a(i)

At this point, one starts the next iteration, meaning that s_i+1⁰ = s_i³. We have thus found the recurrence:

s_i+1⁰ = s_i⁰ + a(i) .

Programs A and B would lead to the same recurrence. Note that adding extraneous statements to the loop (e.g. resetting a(i) to zero after statement 3) would not change the result of symbolic execution, thus showing that this modification does not affect the reduction.

This method is quite powerful and can be extended to handle conditional statements in the loop body [10]. It needs a formal algebra system and its power is directly proportional to the normalization power of this system. However, it cannot handle either reductions on arrays or arrays of reduction (i.e. systems of recurrence equations). The reason is that reference to arrays elements cannot considered as mathematical variables. It is not always true that two occurrences of a[i] refer to the same value, or that an occurrence of a[i] and an occurrence of a[j] refer to different values.

Callahan [2] has proposed a method which can handle systems of reductions provided they are linear (i.e. their solution reduces to matrix products). The basic idea is similar to symbolic execution, but the interpreter handles only linear right hand sides. Variables which are the result of non linear calculations are treated as undefined, and the undefined value has to be propagated across the symbolic calculation. At the end of the process, the linearly computed variables at the end of one iteration are expressed as functions of their values at the beginning of this iteration. Computing their final value is equivalent to the computation of a succession of matrix products, which are associative. Most of the time, the iteration matrix is sparse: Callahan gives methods to exploit this fact in order to minimize the total computation time.

The method of [15] is quite different. The aim here is to normalize the dependence graph of the loop. Since the size of the dependence graph of a loop which is iterated n times is at least O(n), this is impossible in general. The authors propose a limited unfolding of the loop body until periodic patterns become apparent. The recognition of reductions is done on this unfolded graph.

Our aim here is to improve on the symbolic execution method in order to be able to handle reductions on arrays as well. Ideally, the following program

    program D
    real a(0:100)
    s(0,k) = 0.0
    do i = 1,n
        s(i,k) = s(i-1,k) + a(i)
    end do

should have the same normal form as programs A and C.

2.3 Normalization Strategy

Our basic requirement is that the representation of a program must be a well defined mathematical object, to be transformed by applying the usual algebraic rules, the most important one being substitution of equals for equals. This requirement is satisfied in a limited way by symbolic execution: in a basic bloc, the value of a scalar variable after the execution of a statement is a mathematical expression, which can be subjected to ordinary algebraic calculation. This is no longer true if one is interested in arrays and if one wants to handle several loops as a whole.

In that case, one has to switch to a representation by a SARE in the manner of [16]. An object in such a system is the value of a variable at a well defined point in the execution of a program (a statement and a set of counters for the surrounding loops), or equivalently, a point in the domain of one the variables. The system gives relations between these values. Solving the system is equivalent to running the program.

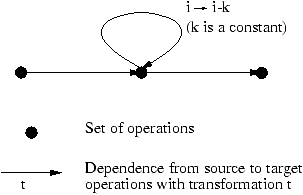
The Dataflow Graph, however is not a sufficiently powerful normal form for reduction recognition. For instance, while programs A and D have the same DFG, this is not true for program C. In fact the DFG's of all simple reductions we want to recognize have a very simple form which is depicted in figure 1.

Figure 1: DFG of a simple reduction

The only circuit ² in the graph is a loop and the dependence function is a translation. If a DFG has circuits which are not loops, we may try to shrink them by eliminating variables by substitution. We will show later that this is not always possible, and give a necessary and sufficient condition for this strategy to succeed. When a loop is found, one tries to identify a reduction by matching the associated equation with a knowledge base. Pattern matching will be discussed in details in Sect. 4.

A program may have a large number of reductions. Once one of them is found, we must set it aside, as it where, and try to find other ones. This may be done simply by introducing a new operator, Scan, which has the same relation to reduction as the integral sign ò has to integration: it allows one to give a name to an object which is not always expressible in closed form within the underlying theory.

In graphical terms, introducing a Scan operator allows one to delete the loop on the corresponding node. When this is done, one may continue eliminating variables until other loops are found. This is best done working from inside outward, as in this way the simplest reductions are detected first.

The result of this analysis is a new version of the Dataflow Graph in which as many reductions as possible have been identified. The result may still be simplified by combining reductions to build higher order reductions. Consider for instance, the program

    program E
    s = 0.0
    do i = 1,n
      do j = 1,i
        s = s + a(i,j)
      end do
    end do

As a first step, we find that the j loop is a sum. The next step is to analyze the i loop, thus finding another summation which uses as data the results of the j loop summations. These results may be combined to give -- we use here the ordinary mathematical notation:

s =

i=1

j=1

a_ij .