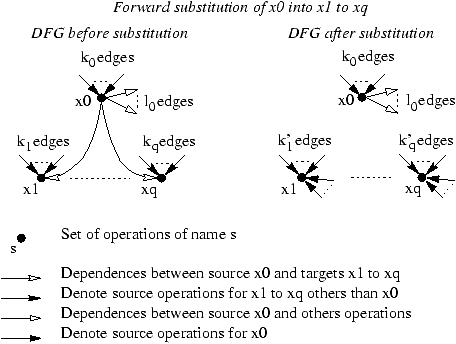
Figure 2: Effect of forward substitution on DFG



The recurrence defined by the system below is a two-variables one:We also want our scan detector to handle scans on multi-dimensional arrays. In this context another problem arises: scans can be computed along very different paths in these arrays. The problem of detecting scans along arbitrary paths seems intractable, hence we deal only with rectilinear ones. An uni-directional scan gathers its data following one vector. An uni-directional scan associated with a multi-dimensional array represents in fact a set of scans:If our pattern matching is directly applied no scan can be detected since there is no self-referencing variable. Our solution is to eliminate either x or y from the system. For example if we replace the reference to y in x by its definition, the result is:x[i] = case i | i = 1 : 0 ; i | 2 <= i <= n : y[i - 1] + a[i] ; esac ; y[i] = case i | i = 1 : 0 ; i | 2 <= i <= n : x[i - 1] + b[i] ; esac ;The variable x is now self-referencing (with stride 2) and a mere pattern matching can point out that x is to be computed by summing the data b[i-1]+a[i]. Going from the first to the second system is not a simple textual substitution, We had to compute the expression y[i-1] from the definition of y in the initial system, then substitute it into the definition of x, then simplify the result by eliminating cases with empty domains. See [19] for details.x[i] = case i | i = 1 : 0 ; i | i = 2 : 0 ; i | 3 <= i <= n : x[i - 2] + b[i - 1] + a[i] ; esac ;
The following program computes a set of scans along the diagonals of the array a:Several detection schemes can be used according to the required precision. The simplest algorithm consists in considering the system of equations as a whole and eliminating as many variables as possible. At this point most of the recurrences are defined by only one variable and a pattern matching can take place. The drawback of this method is that since, as we will see later, removing all circuits in a DFG is not always possible, unguided substitutions may lead into a blind alley, while a more sophisticated algorithm may have found a solution.The uni-directional scan underlying this code has direction (1 , 1) .DO i=1,n DO j=1,n a(i,j)=a(i-1,j-1)+a(i,j) END DO END DO
No scan can be extracted from the following system using this simple scheme:A more complex detection scheme can be designed using multistage eliminations. The principle is to consider only some references (i.e. equations between our multi-dimensional variables). In a first stage only the references related to the innermost loops of the original program are taken into account. This is equivalent to considering the innermost loops as stand-alone programs in which the external loop counters are considered as fixed parameters. Pattern matching is then applied and closed forms are introduced for the detected scans. In the second stage we add to the graph the references relative to the loops just surrounding the innermost ones. A normalization and a pattern matching are performed again and so on. In this way the elimination is obviously more efficient and we can detect more complex scans (see section 4.1). Since closed forms appear during the detection process, pattern matching may be applied on variables already defined by a scan. In most cases this denote a scan whose path is piecewise rectilinear, a multi-directional scan.But the third clause of x and the second of y compute sets of scans. In fact the elimination fails because the recurrences defined by this system are cross-referencing (cannot be computed in parallel).x[i,j] = case i, j | i=1, j=1 : 0 ; i, j | 2<=i<=n, j=1 : y[i-1,m] ; i, j | 1<=i<=n, 2<=j<=m : x[i,j-1] + a[i,j] ; esac ; y[i,j] = case i, j | 1<=i<=n, j=1 : x[i,m] ; i, j | 1<=i<=n, 2<=j<=m : y[i,j-1] + b[i,j] ; esac ;
Our previous example can be handled if the counter i relative to the outermost loop is considered as a parameter. In this context no elimination is to be performed since the only remaining references are the self-referencing ones in the last clauses of x and y. Let sum be the textual equivalent of the å operator, closed forms can be introduced for the scans:A technical issue for the multistage elimination scheme is the characterization of the references to be taken into account. At the SARE level, there is no longer information about the loop nests. We replace the missing information with the help of the concept of reference ``pseudo-depth''. Let the reference to a variable y in an equation for x be of the form:It is very important to note that the closed forms are parametric with respect to i.x[i,j] = case i, j | i=1, j=1 : 0 ; i, j | 2<=i<=n, j=1 : y[i-1,m] ; i, j | 1<=i<=n, 2<=j<=m : x[i,1]+sum(j>=2,a(i,j)) ; esac ; y[i,j] = case i, j | 1<=i<=n, j=1 : x[i, m] ; i, j | 1<=i<=n, 2<=j<=m : y[i,1]+sum(j>=2,b(i,j)) ; esac ;
|
The substitution process terminates when no more variable can be eliminated. The process succeeds if, in the terminal system, all circuits are loops.
Figure 2: Effect of forward substitution on DFG
In the context of linear equations, systems such as (2) can always be solved. This is due to the fact that the Gaussian elimination algorithm use substitutions and also linear simplification. Linear simplification is a powerful tool since it can remove loops from the system graph. For example in the graph of the system below there is a loop on the vertex x1:The criterion is also valid for a SARE. Its graph is more complex since some edges are defined only in a sub-domain of the variable definition domain. This has an influence on the elimination process. After a substitution, new edges domains are computed by intersection of the old domains. If this intersection is void, the edge does not really exist. Hence the criterion is always sufficient but no longer necessary. One may also say that the criterion is sufficient and necessary if no simplification of the clause domains occurs.After simplification of the first equation (x1=-1/3x2) there is no longer a loop on x1.
ì
í
î
x1=4.x1+x2 x2=2.x1 .
If a basic substitution is applied to a strongly connected graph, there is no circuit including x0 and the resulting graph restricted to all vertices but x0 is also strongly connected.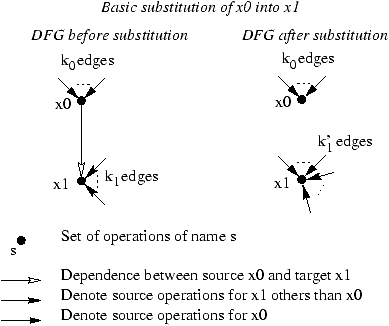
Figure 3: Effect of basic forward substitution on DFG
The system associated to the program belowisDO i=1,2*n a(i)=a(2*n-i+1) END DOWe name the clauses using the name of the variable and their rank in the variable definition. For instance the first clause of x is x.0. If x is included in a strong component, an elimination process may fail because of the loop in the variable graph. In contrast the clause graph does not have this loop, and so the elimination process may go further (see figure 4).x[i] = case i | 1<=i<=n : a[2*n-i+1] ; i | n+1<=i<=2*n : x[2*n-i+1] ; esac ;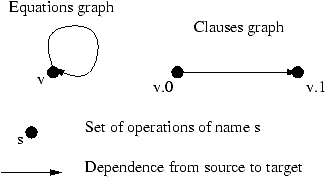
Figure 4: Example of difference between equation graph and clause graph


