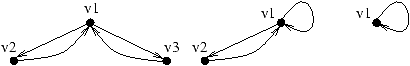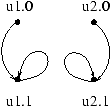Montrons, sur un exemple, comment notre algorithme basé sur des
substitutions simples trouve les sommets par lesquels passent tous
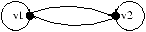
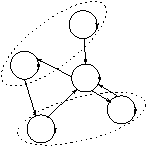
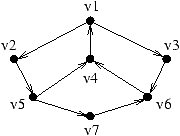
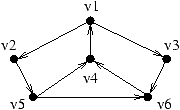
les circuits d'une composante fortement connexe. Le graphe de
départ est donné ci-dessous.
Il faut noter que l'heuristique échoue sur ce graphe à cause des
cycles parasites.
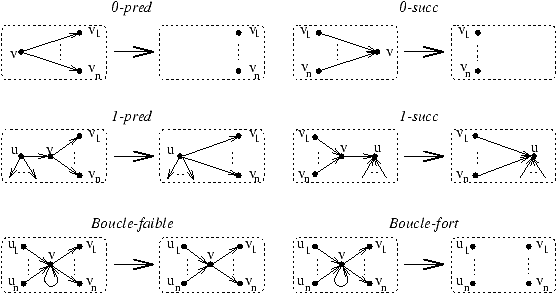
Tous les tableaux utilisés par l'algorithme (7) sont
donnés ici comme une liste de couples constitués d'un indice et de
la valeur correspondante. Le tableau des prédécesseurs pred
est donc :
pred={ (v1,{v4}) (v2,{v1}) (v3,{v1}) (v4,{v5 v6})
(v5,{v2}) (v6,{v3 v7}) (v7,{v5}) }
Le tableau du nombre de successeurs ns initial est :
ns={ (v1,2) (v2,1) (v3,1) (v4,1) (v5,2) (v6,1) (v7,1) }
Quand au tableau succ il peut être initialisé à :
succ={ (v1,v2) (v2,v5) (v3,v6) (v4,v1) (v5,v4) (v6,v4) (v7,v6) }
Au vu de ns les valeurs empilées dans p sont :
p={ v7 v6 v4 v3 v2 }
Le premier sommet avec un seul successeur que l'algorithme considère
est v7. Sa liste de prédécesseurs ne comporte pas d'élément
commun avec celle de son successeur v6.
Les nouveaux tableaux des prédécesseurs et du successeur privilégié
sont :
pred={ (v1,{v4}) (v2,{v1}) (v3,{v1}) (v4,{v5 v6}) (v5,{v2}) (v6,{v3 v5}) }
succ={ (v1,v2) (v2,v5) (v3,v6) (v4,v1) (v5,v6) (v6,v4) }
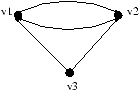
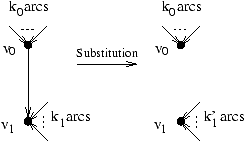
Intuitivement le sommet v7 vient d'être retiré de la composante
fortement connexe comme indiqué sur le schéma ci-dessous :
Le nouveau sommet considéré est v6, la liste de ses
prédécesseurs comprend un élément qui se retrouve dans celle
de v4, il s'agit du sommet v5. En conséquence le nombre de
successeurs de v5 passe à 1 et v5 est empilé sur p.
Les nouvelles variables de l'algorithme sont :
pred={ (v1,{v4}) (v2,{v1}) (v3,{v1}) (v4,{v3 v5}) (v5,{v2}) }
ns={ (v1,2) (v2,1) (v3,1) (v4,1) (v5,1) }
succ={ (v1,v2) (v2,v5) (v3,v4) (v4,v1) (v5,v4) }
p={ v5 v4 v3 v2 }
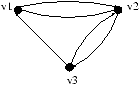
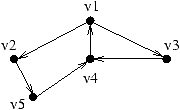
Le sommet v6 à été éjecté de la composante fortement connexe :
Notons qu'à ce niveau de l'algorithme l'heuristique découvre que
v1 est un transversal.
Le sommet à traiter est désormais v5. Sa liste pred ne
contient pas d'élément commun avec celle de son successeur v4,
le tableau ns est donc inchangé. Les nouveaux tableaux pred
et succ sont :
pred={ (v1,{v4}) (v2,{v1}) (v3,{v1}) (v4,{v2 v3}) }
succ={ (v1,v2) (v2,v4) (v3,v4) (v4,v1) }
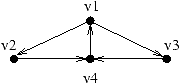
La composante fortement connexe réduit encore :
Les dernières étapes sont données sur le schéma ci-dessous :
Finalement seul le sommet v1 reste dans la composante fortement
connexe : c'est le transversal minimal du graphe initial.
Considérons le calcul d'un produit de matrices 2x2 :
v1 : { i | 1 <= i <= n } of real ;
v2 : { i | 1 <= i <= n } of real ;
v3 : { i | 1 <= i <= n } of real ;
v4 : { i | 1 <= i <= n } of real ;
v1[i] = case
{ i | i = 1 } : a[1,1] ;
{ i | i >= 2 } : v1[i-1]*a[1,1]+v2[i-1]*a[1,2] ;
esac ;
v2[i] = case
{ i | i = 1 } : a[1,2] ;
{ i | i >= 2 } : v1[i-1]*a[1,1]+v2[i-1]*a[1,2] ;
esac ;
v3[i] = case
{ i | i = 1 } : a[2,1] ;
{ i | i >= 2 } : v3[i-1]*a[2,1]+v4[i-1]*a[2,2] ;
esac ;
v4[i] = case
{ i | i = 1 } : a[2,2] ;
{ i | i >= 2 } : v3[i-1]*a[2,1]+v4[i-1]*a[2,2] ;
esac ;
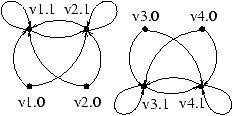
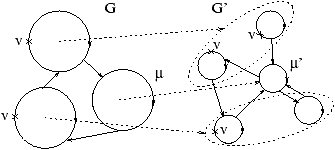
Même le graphe des clauses d'un tel système n'est pas
normalisable par des substitutions :
En effet les circuits de la composante fortement connexe formée de
v1.1 et de v2.1 ne passent pas par un même sommet. Idem
pour la composante incluant v3.1 et v4.1.
Par contre, les quatre équations ont le même domaine de définition
(c'est logique puisqu'elles proviennent du même nid de boucles) et les
dépendances sont toutes de profondeur 0. Il est donc valide de fusionner
v1 et v2, ainsi que v3 et v4.
Il n'y a pas de problème de génération des domaines des clauses pour les
nouvelles équations car les domaines des clauses des anciennes équations
sont analogues. Si x est un opérateur qui forme des couples à
partir de deux vecteurs de scalaires, le système après fusion s'écrit :
u1 : { i | 1 <= i <= n } of real x real ;
u2 : { i | 1 <= i <= n } of real x real ;
u1[i] = case
{ i | i = 1 } : a[1,1] x a[1,2] ;
{ i | i >= 2 } :
( proj(u1[i-1],1)*a[1,1]+proj(u1[i-1],2)*a[1,2] ) x
( proj(u1[i-1],1)*a[1,1]+proj(u1[i-1],2)*a[1,2] ) ;
esac ;
u2[i] = case
{ i | i = 1 } : a[2,1] x a[2,2] ;
{ i | i >= 2 } :
( proj(u2[i-1],1)*a[2,1]+proj(u2[i-1],2)*a[2,2] ) x
( proj(u2[i-1],1)*a[2,1]+proj(u2[i-1],2)*a[2,2] ) ;
esac ;
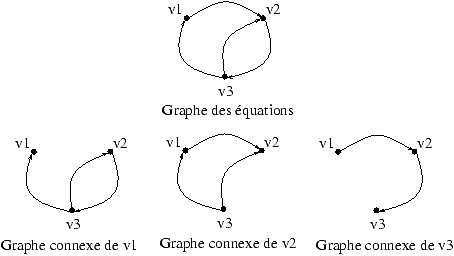
Le système est alors en forme normale ; pour s'en convaincre il suffit
de regarder le graphe du système :
La reconnaissance de forme peut donc être appliquée sur l'expression
de u1.1 et sur celle de u2.1. Si une règle sur le produit
matrice-vecteur est prévue, la détection de la multiplication de
matrices se fait sous la forme de deux de ces produits.
Une remarque importante est que la fusion de clauses est impossible ;
en effet les références dans le système d'équations se font
aux variables définies par les équations. Il n'est donc pas
possible de changer uniquement le type des valeurs calculées par
une clause ; il faut changer le type des valeurs pour toute l'équation.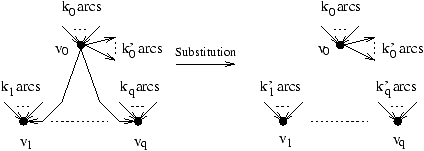




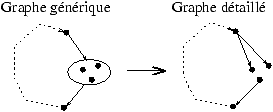

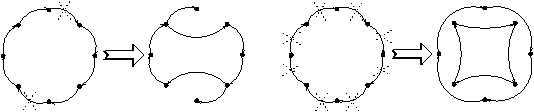
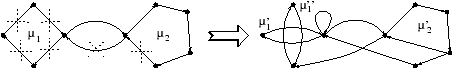


 Finalement seul le sommet v1 reste dans la composante fortement connexe : c'est le transversal minimal du graphe initial.
Finalement seul le sommet v1 reste dans la composante fortement connexe : c'est le transversal minimal du graphe initial.