Écriture symbolique des réductions et des scans

Chapter 10

Écriture symbolique des réductions et des scans

Lorsqu'un scan est détecté nous le traduisons sous une forme condensée de la même façon que le résultat d'une intégration peut s'exprimer à l'aide d'un signe "intégrale" (i.e. ò). L'avantage de mettre les scans sous une forme condensée est double :

cela permet la détection de scans multi-directionnels (e.g. une somme double) ;
cela simplifie la manipulation des scans dans les traitements ultérieurs (calcul de la base de temps, génération de code).

Dans ce chapitre nous commençons par lister les différentes notations utilisées dans certains langages pour exprimer des scans. Ces notations ne conviennent pas pour exprimer les scans calculés dans les programmes impératifs aussi il a été nécessaire d'introduire notre propre opérateur : l'opérateur Scan. Une comparaison entre cet opérateur et les autres notations est présentée en fin de chapitre.

10.1

Opérateurs de réductions et de scans classiques

Certains langages comportent déjà des opérateurs de récurrences. En fait de nombreux langages utilisés dans le domaine de la conception de circuits systoliques incluent des opérateurs de réduction à la APL. Le langage Crystal (voir [44]) dispose des opérateurs \_L, \_R et \_B. Ces opérateurs travaillent sur un ensemble ordonné de valeurs. La réduction peut être faite de la gauche vers la droite avec l'opérateur \_L, dans le sens inverse avec \_R ou suivant un arbre binaire de calcul avec \_B.

En Crystal, le calcul de la somme des éléments du tableau a s'écrit :
\_L + [a(1),...,a(n)] .

Le langage Alpha (voir [41]) dispose de l'opérateur red. Cet opérateur travaille sur un ensemble non ordonné de valeurs mais autorise une partition de ces valeurs ce qui permet d'effectuer un ensemble de réductions et non pas seulement une réduction isolée.

Ainsi l'expression Alpha ci-dessous calcule les sommes des lignes de la matrice a :

a : { i,j | 1<=i<=n, 1<=j<=n } of real ; red( +, (i,j ->i), a[i,j] ) ;

La sémantique des langages Lacs [53] et Pei [63] leur permet d'exprimer directement des réductions. L'environnement de programmation Pei ne possède pas à proprement parler d'opérateur de réduction, mais une notion de fonctions inverses qui permet là aussi de partitionner un ensemble de valeurs [23]. Une fonction associative et commutative est alors appliquée sur les partitions pour réaliser la réduction. L'environnement Pei manipule des champs de données qui sont analogues aux variables spatiales de Alpha. Soit X un champ de données de type V sur Zⁿ ; la partition peut se faire soit par rapport aux valeurs de ce champ (il s'agit d'un inverse fonctionnel de X), soit par rapport aux positions des valeurs dans l'espace Zⁿ (il s'agit alors d'un inverse géométrique de X). Les réductions classiques sont construites à partir d'un inverse géométrique. Plus précisément, si g est une fonction de Zⁿ dans Zⁿ, l'inverse géométrique d'un champ de données X sur Zⁿ par g est le champ de données de domaine g( D) où D est le domaine de X. De plus à chaque point z de g( D) est associé l'ensemble (non ordonné) des valeurs de X associées à un point z' de D tel que g(z')=z.

Prenons l'exemple déjà utilisé pour red, à savoir le calcul des sommes des lignes d'une matrice. Pour exprimer ces réductions en Pei nous supposons qu'il existe un champ de données A de forme carrée contenant les valeurs de a. Nous supposons aussi qu'il existe une fonction sum calculant la somme d'un ensemble de valeurs. Il faut ensuite définir la fonction de partitionnement :
path = \(i',j') | ( 1<=i'<=n, 1<=j'<=n ) . (i',n)
La fonction path est écrite ici avec les notations Pei. Son domaine de définition ( 1<=i'<=n, 1<=j'<=n ) est la matrice entière, et elle associe à (i',j') la valeur (i',n). L'inverse géométrique se note à l'aide de l'opérateur ;>, dans ce contexte le calcul des sommes s'écrit :
S = sum |> path ;> A

La détection de récurrences demande plus qu'un opérateur de réduction. Un opérateur de scan est nécessaire. Les langages Crystal et Lacs possèdent de tels opérateurs.

Ainsi l'expression Crystal
s=\\ + [a(1),...,a(n)] .
et l'expression Lacs
{ i | 1<=i<=n: { i' | 1<=i'<=i: a[i'] } +=> s[i] }
calculent le même vecteur s=[s₁,...,s_n] où s_i=å_k=1ⁱ a(k) .

Il existe un (futur) langage de programmation pour machines parallèles qui présente des opérateurs de réduction et de scan évolués. Il s'agit de HPF. En fait un opérateur de réduction est introduit par fonction binaire associative, mais la sémantique de calcul est la même pour toutes les primitives. Décrivons d'abord l'opérateur de réduction XXX_SCATTER. Tout comme l'opérateur Scan la primitive calcule un ensemble de réductions. Elle prend comme paramètres :

un tableau a qui contient les données à réduire ;
un tableau b qui contient les valeurs initiales des réductions ;
un ensemble de tableaux d'indirection x₁ à x_n de même dimension que a, où n est la dimension du tableau b.

En supposant que la fonction binaire utilisée par la réduction soit o, un élément du tableau résultat est :

u(i₁,...,i_n)=b(i₁,...,i_n)o

(j₁,...,j_m) | " kÎN_n^*, x_k(j₁,...,j_m)=i_k

a(j₁,...,j_m) .

En HPF, notre exemple de calcul des sommes des lignes d'une matrice s'écrit (dans le cas où n=5) :

SUM_SCATTER(a,[0 0 0 0 0], é
ê
ê
ê
ê
ë

1 1 1 1 1

2 2 2 2 2

3 3 3 3 3

4 4 4 4 4

5 5 5 5 5
ù
ú
ú
ú
ú
û ) .

Les opérateurs de scan de HPF ont eux un pouvoir d'expression assez limité. En effet XXX_PREFIX et XXX_SUFFIX ne permettent de calculer des scans que suivant une direction, cette direction devant être une dimension du tableau.

10.2

Sémantique de l'opérateur Scan

Si certains des langages étudiés ci-dessus permettent d'exprimer des ensembles de scans simples aucun ne permet d'exprimer des scans dont l'espace d'accumulation est une ligne brisée. Or ces scans se rencontrent dans les systèmes d'équations issus de programmes impératifs. Nous avons donc mis au point notre propre forme condensée. Cette forme s'écrit :

Scan( D

,(e_i)

iÎ{1,...,k}

,b,d,g) .

L'espace d'accumulation du scan (y compris le domaine des valeurs initiales) est D, ses vecteurs directeurs sont les (e_i), b est une opération binaire associative, enfin d et g représentent les données et les valeurs d'initialisation du scan.

Avec l'opérateur Scan, le calcul des sommes partielles des n éléments d'un vecteur a s'écrit donc de la façon suivante :
Scan( N_n^*, [1],+,l i.a(i),a(1)) ] .
En utilisant le fait que 0 est l'élément neutre pour l'addition, cette somme peut aussi s'écrire :
Scan(N_n, [1],+,l i.a(i),0) .

Pour donner une sémantique précise de la forme condensée, nous introduisons un dérivé du minimum lexicographique ne concernant que certaines directions d'un convexe :

min

e₁,...,e_k

(z)= z-

i=1

n_i.e_i où

(n₁,...,n_k)= lexmax(µ₁,...,µ_k | (µ₁,...,µ_k)ÎN

^k, z-

i=1

µ_i.e_iÎ D)

(la fonction lexmax représente le maximum lexicographique d'un ensemble de vecteurs). Un maximum est défini de la même manière :

max

e₁,...,e_k

(z)= z+

i=1

n_i.e_i où

(n₁,...,n_k)= lexmax(µ₁,...,µ_k | (µ₁,...,µ_k)ÎN

^k, z+

i=1

µ_i.e_iÎ D)

Que ce soit pour le minimum min_e_₁_,...,e_{_k}^D(z), ou pour le maximum max_e_₁_,...,e_{_k}^D(z), quand le maximum lexicographique n n'existe pas, la valeur de l'extremum est fixé à ^. Cela peut arriver, par exemple, si z n'est pas dans le convexe D.

Dans ce contexte, l'expression (9.1) calcule un tableau multi-dimensionnel v de même structure que D dont les valeurs sont données par l'équation suivante :

" zÎ D, v(z)=

ì
ï
ï
ï
ï
ï
ï
í
ï
ï
ï
ï
ï
ï
î

z=min

e₁,...,e_k

(z)

g(z)

sinon si

z=min

e₂,...,e_k

(z)

f(z,v(max

e₂,...,e_k

(z-e₁)))

...

sinon si

z=min

e_k

(z)

f(z,v(max

e_k

(z-e_k-1)))

sinon

f(z,v(z-e_k)) .

La fonction f qui apparait dans l'équation précédente est :

f=l zx.b(x,d(z)) .

Intuitivement, cette définition signifie que la fonction de propagation f est appliquée suivant un parcours précis dans le domaine d'accumulation D. Le parcours est défini par les vecteurs directeurs de l'opérateur Scan ; s'il existe un seul vecteur directeur, il s'agit d'une droite, sinon il s'agit d'une ligne brisée.

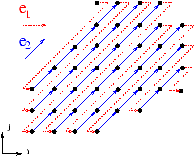
Prenons un exemple de parcours bi-directionnel de vecteurs directeurs e₁=[1,0] et e₂=[1,1]. Le parcours est représenté sur le schéma ci-dessous :

Le domaine d'accumulation est l'ensemble des disques noirs. En un mot, le parcours est réalisé en suivant d'abord le dernier vecteur directeur (ici e₂). Lorsque le parcours rencontre la limite du convexe, il s'écarte de la trajectoire courante en utilisant le vecteur directeur précédent (ici e₁) et en se ramenant sur la limite ``inférieure'' du convexe au sens des derniers vecteurs directeurs (ici seulement e₂). Le parcours reprend alors normalement (ici en utilisant e₂).

Tel qu'il vient d'être défini l'opérateur Scan permet d'exprimer la plupart des scans (et donc des réductions) d'un programme à contrôle statique.

Le programme Fortran
DO i=1,n
  DO j=1,m
    DO k=1,l
      s(i,j,k)=s(i,j-1,k-1)+s(i,j,k)
    END DO
  END DO
END DO
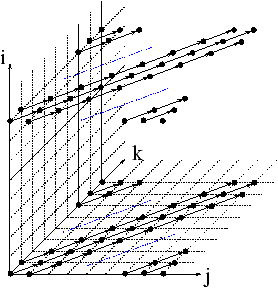
s'exprime facilement avec un opérateur de récurrence :
Scan( { i,j,k | 1<=i<=n, 0<=j<=m, 0<=k<=l }, ( [0 1 1] ),
      +, s[i,j,k], s[i,j,k] )
Nous écrirons les opérateurs scans à la Alpha. De plus, pour simplifier les notations, nous convenons que le prédicat définissant D et les fonctions f et g partagent le même l préfixe ; celui-ci n'est écrit qu'une seule fois dans l'expression de D sous la forme {i₁,...,i_n | ...}. Les dépendances de ce scan sont illustrées par le schéma ci-dessous.

En fait, l'opérateur Scan a une puissance d'expression sous-employée dans le cadre de la détection de récurrences. Il serait intéressant de l'intégrer dans un langage de description de systèmes d'équations.

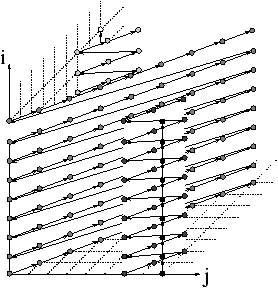
Par exemple l'opérateur Scan
Scan( { i,j,k | 1<=i<=n, 0<=j<=m, 0<=k<=l }, ( [1 0 0] [0 1 1] ),
      +, s[i,j,k], s[i,j,k] )
décrit un ensemble de scans bi-directionnels relativement complexes. En fait il s'agit de l'opérateur Scan de l'exemple précédent auquel un vecteur directeur a été ajouté : [1 0 0]. Comme le montre le schéma ci-dessous, les scans ne sont plus calculés suivant des lignes diagonales par rapport à (j,k) mais suivant des plans diagonaux par rapport à (j,k) (sur le schéma seuls quelques plans ont été représentés).

Ce scan peut provenir d'un programme Fortran.
DO i=1,n
  DO j=1,m
    DO k=1,l
      IF ((i.GE.1).AND.(j.EQ.0)) THEN
        s(i,j,k)=s(i-1,m,m-j)+s(i,j,k)
      ELSE IF ((i.GE.1).AND.(k.EQ.0)) THEN
        s(i,j,k)=s(i-1,l-k,l)+s(i,j,k)
      ELSE
        s(i,j,k)=s(i,j-1,k-1)+s(i,j,k)
      END IF                        
    END DO
  END DO
END DO
Mais ce n'est pas une façon de programmer très naturelle.

Terminons cette section par une remarque d'ordre pratique. Du point de vue de l'implantation, le dernier paramètre d'un opérateur Scan (i.e. les valeurs initiales de la récurrence) est stocké sous la forme d'une équation. Si les domaines des clauses de cette équation sont bien des convexes disjoints, leur union n'est pas forcément un convexe comme dans le cas d'une équation régulière. Ceci vient du fait que l'ensemble

{ z | z=min

e₁,...,e_k

(z) } ,

n'est pas, en général, convexe.

10.3

Comparaison des diverses notations

Dans cette section nous comparons notre opérateur Scan aux diverses notations de scans présentées en début de chapitre.

Comme les opérateurs de réductions de Crystal possèdent une notion d'ordre, ils sont définis, comme l'opérateur Scan, même pour des fonctions binaires non commutatives. Il est intéressant de constater qu'un opérateur Scan uni-directionnel utilisé en tant que réduction

Scan( { i | 0 <= i <= n }, ( [1] ), b, d, g)[n]

peut s'écrire en Crystal :

\_L b [g 0,d 1,...,d n] .

L'opérateur Scan ne peut pas effectuer de calcul selon un arbre binaire comme l'opérateur \_B. D'un autre coté, les opérateurs de Crystal présentent un inconvénient majeur ; ils ne permettent pas de spécifier un ensemble de réductions.

L'opérateur red du langage Alpha, permet lui d'exprimer un ensemble de réductions mais il travaille sur des valeurs non ordonnées. Il est donc limité à des fonctions binaires commutatives mais surtout peut difficilement être utilisé dans notre contexte car une propriété importante de nos variables spatiales (les équations) est qu'elle héritent de l'ordre du programme source. Par contre les récents travaux visant à introduire dans Alpha la notion de décomposition des variables spatiales (e.g. une matrice peut être vue comme un vecteur de vecteurs) permettent une plus grande liberté d'expression. Un opérateur Scan donné pourra alors être exprimé en Alpha, mais les notations risquent d'être un peu plus lourdes.

Il faut noter que la démarche de Pei concernant les réductions est la démarche inverse d'une détection de réductions dans un programme impératif. Dans l'environnement Pei, le programmeur définit sa réduction à l'aide de l'opérateur ;> puis, par raffinements successifs, construit un programme déterministe. En effet, une réduction exprimée à l'aide d'un inverse géométrique n'est pas déterministe dans la mesure où l'ordre d'application de l'opérateur associatif et commutatif n'est pas spécifié. Les raffinements vont consister à écrire la fonction d'inversion comme une composée de fonctions bijectives puis à réécrire le programme Pei sans utiliser l'opérateur ;>.

Reprenons l'exemple de réduction en Pei décrit à la section 9.1. La fonction path de cet exemple est obtenue en composant plusieurs fois la fonction succ ci-dessous avec elle-même.
succ = \(i',j') | ( 1<=i'<=n, 1<=j'<=n-1 ) . (i',j'+1)
Des règles de réécriture permettent de transformer l'expression initiale des réductions en une nouvelle expression Pei :
T = ( succ ;> T ) /+/ A
S = sum |> ( T <| \(i',j') | (j'=n) )
Ces équations définissent désormais le calcul par récurrence en décalant plusieurs fois la matrice A vers la droite. L'effet de l'opérateur /+/ est de superposer les valeurs de deux champs. En définitive le champ contient pour j'=n toutes les valeurs d'une ligne superposées. Il suffit alors de resteindre ce champ à la dernière colonne et d'appliquer une somme sur les valeurs superposées. Comme la fonction succ est bijective il est même possible de supprimer les opérateurs ;> et de les remplacer par l'opérateur <| qui opére un déplacement de la position des valeurs d'un champ. L'expression Pei raffinée est alors :
T = ( T <| pred ) /+/ A
S = sum |> ( T <| \(i',j') | (j'=n) )
Le fonction pred est l'inverse de la fonction succ, c'est-à-dire, en Pei :
pred = \(i',j') | ( 1<=i'<=n, 2<=j'<=n ) . (i',j'-1)

Il s'agit bien là d'une démarche inverse de celle de la détection de réductions, dans laquelle il faut suivre un chemin d'accumulation défini par l'ordre du programme séquentiel pour en extraire les réductions. L'approche de Pei est quasiment impossible à automatiser puisqu'il s'agit de trouver un chemin de manière intuitive ; c'est au programmeur de définir ce chemin. Dans la détection de réductions les ``raffinements'' peuvent être automatisés car il s'agit de déductions et non pas d'inductions. La détection présentée dans cette thèse peut être vue comme l'enchainement automatique d'anti-raffinements à la Pei pour aboutir à une représentation condensée des scans. Nous parlons d'anti-raffinements puisque nous utilisons les raffinements de Pei à rebours.

Les primitives XXX_SCATTER du langage HPF permettent de calculer toutes les réductions exprimées à l'aide d'un opérateur Scan (sous reserve que la fonction binaire désirée soit disponible). Il suffit que sur une ligne brisée d'accumulation les tableaux d'indirection rendent le même vecteur de taille n (ce vecteur doit être différent des vecteurs associés aux autres lignes brisées).

Les sommes calculées par l'opérateur Scan
Scan( { i,j | 1<=i<=5, 1<=j<=5 }, ( [1 1] ), +, d, d)
le sont aussi par l'instruction

SUM_SCATTER(d,[0 0 0 0 0 0 0 0 0], é
ê
ê
ê
ê
ë

1 2 3 4 5

2 3 4 5 6

3 4 5 6 7

4 5 6 7 8

5 6 7 8 9
ù
ú
ú
ú
ú
û ) .
Les tableaux résultats n'ont pas la même dimension mais il est tout aussi facile d'écrire un SUM_SCATTER avec deux tableaux d'indirection pour que les 5 premières sommes soient stockées dans la première colonne de la matrice résultat et les 5 dernières dans la dernière ligne de la même matrice.

Cependant la notation est lourde (il faut remplir les tableaux d'indirection) et surtout trop générale. Il serait, par exemple, intéressant de savoir comment les compilateurs optimiseront des réductions calculées sur des cercles concentriques dans une matrice. Nous préférons nous en tenir à notre opérateur qui, s'il est moins puissant, est parfaitement manipulable par les outils classiques de l'algèbre linéaire et par des opérations sur les convexes.

En ce qui concerne les scans, l'opérateur \\ de Crystal n'a pas de mécanisme spécifique pour désigner des ensembles de scans. Par contre le langage Lacs permet d'exprimer de tels ensembles.

Par exemple, l'opérateur Scan
u=Scan( { i,j | 1<=i<=n, 1<=j<=n }, ( [1 1] ), +, d, d)
peut être traduit en Lacs, cela donne l'expression
{i,j | 1<=i<=n,1<=j<=n: {i',j' | 1<=i'<=i,1<=j'<=j: d i' j'} +=> u[i,j]}
Il est à noter que l'expression Lacs met en relief l'ensemble des valeurs nécessaires au calcul d'un u[i,j]. Cet ensemble est d'ailleurs nécessaire au calcul de la base de temps de l'opérateur (voir la définition de l'ensemble D dans la section 11.3).

Enfin, ces scans d'HPF sont trop limités pouvoir être utilisé dans le cadre de la détection de récurrences. En effet, les scans doivent être calculés suivant les directions canoniques des tableaux.

En conclusion, très peu de notations peuvent décrire un ensemble paramétrique de scans de façon compacte (i.e. à notre connaissance uniquement le langage Lacs). De plus aucune ne sait traiter le cas des scans multi-directionnels. C'est la raison pour laquelle nous avons introduit notre propre opérateur.